【深層学習】マルチタスク学習でオッズと着順を予測する競馬AI¶
0-1.本Notebookの立ち位置¶
マルチタスク学習を深層学習で行う競馬予想AIの作成方法を解説していきます。
これまでは深層学習の基本をおさえるため、PyTorchを使った深層学習モデル作成手順を解説してきました。
チュートリアルで扱った項目は以下
- 【初学者対象】深層学習 超解説
- 深層学習の基本的な知識
- 深層学習の学習過程
- 【全解説】深層学習で必要なデータ前処理
- データセット作成
- 深層学習でLightGBMの特徴量重要度的なものを出す方法
- PyTorchのモデル構築方法
- 学習・推論の実行
- モデルの解釈方法
- モデル保存
よって、基本は上記チュートリアルをベースにした実装をしていくので、深層学習よくわからないという方は、上記の3記事参照されることをお勧めします
0-2.前提環境¶
使用する深層学習ライブラリの紹介です。
- Python 3.10.5
- PyTorch 2.3.1
- GPU使う場合は:CUDA 11.8
ない場合はpip等でインストールしてください。
0-3.宣伝(環境準備)¶
本講座で扱うソースでは一部秘匿させていただいております。
ソースは「ゼロから作る競馬予想モデル・機械学習入門」にあるものを使用しています。
また、本Notebookは「dev-um-ai > notebook > DeepLearning > 0000-4_deeplearning_tutrial4.ipynb」にあります。
環境構築(パッケージ管理)はpoetryを使用しているので、プロジェクトファイルさえあればコマンド一発で環境構築が完了するので、ぜひご活用ください。
Bookersアカウントとご自身のYouTubeアカウントを連携していただき、以下のチャンネルを登録して頂きますと1000円引きで入手出来ますのでぜひ登録よろしくお願いいたします。
1. マルチタスク学習とは?¶
本Notebookは実装方法の解説を主な目的としています。
そのため、マルチタスク学習そのものの説明は以下の記事に預けることとします。
2.チュートリアルのデータセット読込み¶
まずはチュートリアルで作成したデータセットを読み込みます。
import numpy as np
import random
from torch.utils.data import Dataset
import torch
import pandas as pd
import pathlib
import pickle
import warnings
import sys
sys.path.append(".")
sys.path.append("../..")
from src.data_manager.dataset_tools import DatasetDict # noqa
# Datasetクラスを継承してカスタムDatasetクラスを作成
class CustomKaibaAIDataset(Dataset):
def __init__(self, dfnum: pd.DataFrame, dfcat: pd.DataFrame, dflabel: pd.Series) -> None:
self.numerous = dfnum
self.cat = dfcat
self.label = dflabel
def __len__(self):
return len(self.label)
def __getitem__(self, index):
num_fea = torch.tensor(self.numerous.loc[index], dtype=torch.float32)
# カテゴリ特徴量は一つ一つベクトル埋め込み層に突っ込むので、特徴量ごとに分けてtensor化しておく
cat_feas = torch.tensor([self.cat[c].loc[index]
for c in self.cat.columns], dtype=torch.float32)
label = torch.tensor(self.label[index], dtype=torch.float32)
return num_fea, cat_feas, label
cache_dir = pathlib.Path("./data")
with open(cache_dir / "dataset_mapping.pkl", "rb") as f:
dataset_mapping: dict[str, DatasetDict] = pickle.load(f)
def set_seed(seed):
random.seed(seed) # Python標準の乱数シード
np.random.seed(seed) # NumPyの乱数シード
torch.manual_seed(seed) # PyTorchの乱数シード(CPU用)
if torch.cuda.is_available():
torch.cuda.manual_seed(seed) # CUDAの乱数シード(単一GPU用)
torch.cuda.manual_seed_all(seed) # 複数GPU用
# 再現性のためにPyTorchの動作設定を変更
torch.backends.cudnn.deterministic = True
torch.backends.cudnn.benchmark = False
# シードを固定
set_seed(42)
# モデル作成で使用する特徴量
# 量的変数の特徴量
num_feas = [
'distance_dev',
'number_dev',
'boxNum_dev',
'age_dev',
'jweight_dev',
'weight_dev',
'gl_dev',
'race_span_fill_dev',
] + ['winR_stallion', 'winR_breed', 'winR_bStallion', 'winR_b2Stallion']
# 質的変数の特徴量
cat_feas = [
'place_en',
'field_en',
'sex_en',
'condition_en',
'jockeyId_en',
'teacherId_en',
'dist_cat_en',
'horseId_en',
"raceGrade", "stallionId_en", "breedId_en", "bStallionId_en", "b2StallionId_en"
]
3.データセットの修正¶
マルチタスク学習を行うため、ラベルと特徴量のデータセットを修正する必要があります。
今回作成するサードモデルの根幹は、以下の二つのタスクを学習するものです。
- オッズの推定
- 着順の推定
よって、モデルの入出力を以下のようにします。
- 入力
全出走馬の特徴量の2次元配列 - 出力
- 出力1: オッズに基づく勝率
- 出力2: 1着の確信度
サードモデルではレースごとにオッズの勝率の分布と着順を推定していたので、入力に出走馬全部の情報を使うようにする。
期待する効果として以下を上げる。
- セカンドモデルまでは1頭ごとに1着になるかどうかを判断するモデルになっていたため、サードモデルでは他の出走馬も考慮した予測をすること
- オッズの推定とオッズの勝率の分布を推定するので、的中率と回収率の両方を考慮したモデルになること
よって、まずはデータセットを2次元テンソルにできるように、raceIdごとに統一のインデックスを割り振るようにします。
また、oddsの勝率を扱うので、その分の特徴量も作っておく
for key, dataset in dataset_mapping.items():
for mode in ["train", "valid", "test"]:
idf: pd.DataFrame = dataset.__dict__[mode]
raceId_map = idf.sort_values(
["raceDate", "raceId"])[["raceId"]].drop_duplicates(
ignore_index=True).reset_index(
names="rst_idx").set_index("raceId")["rst_idx"].to_dict()
idf.index = idf["raceId"].map(raceId_map).tolist()
idf["odds_rate"] = 0.8/idf["odds"]
idf["odds_rate"] /= idf["raceId"].map(
idf[["raceId", "odds_rate"]].groupby("raceId")["odds_rate"].sum().to_dict())
dataset_mapping[key].__dict__[mode] = idf.copy()
データセットを2次元テンソルとして取り出すために、Datasetクラスを作り直す。
2次元テンソルは、固定長である方が都合が良い。
もともと2次元テンソルにするのは、出走馬すべての特徴量を行列にしたものなので、2次元テンソルのサイズは18行で固定するとよさそう。
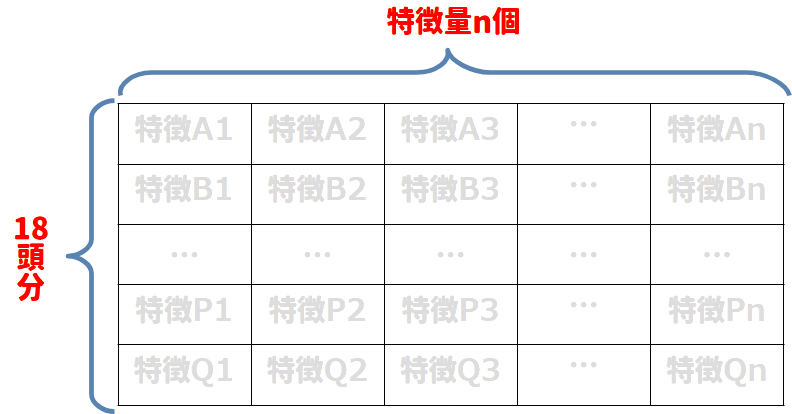
ただ、すべてのレースが18頭立てのレースになっているわけではないため、そのようなレースについては18行分のデータになるまでパディングするようにする。
パディングする処理は、Datasetクラス側で行うようにする。
from typing import Literal
class CustomKaibaAIDatasetForMultiTask(Dataset):
def __init__(self, idf: pd.DataFrame, num_feas: list[str], cat_feas: list[str]) -> None:
self.static_length = 18
idxlist = []
for k, v in (self.static_length-idf.index.value_counts()).sort_index().to_dict().items():
idxlist += [k]*v
dfnum_pad = pd.DataFrame(0, index=idxlist, columns=num_feas)
dfcat_pad = pd.DataFrame([dataset.cat_num_list] *
len(idxlist), index=idxlist, columns=cat_feas)-1
dfpad = pd.concat([dfnum_pad, dfcat_pad], axis=1)
idf2 = pd.concat([idf, dfpad]).loc[list(
range(idf.index.nunique()))]
self.numerous = idf2[num_feas]
self.cat = idf2[cat_feas]
self.label = idf2["label"].fillna(19)
self.odds_rate = idf2["odds_rate"].fillna(0)
def __len__(self):
return self.label.index.nunique()
def __getitem__(self, index):
num_feas = torch.tensor(
self.numerous.loc[index].values, dtype=torch.float32)
# カテゴリ特徴量は一つ一つベクトル埋め込み層に突っ込むので、特徴量ごとに分けてtensor化しておく
cat_feas = torch.tensor(
self.cat.loc[index].values, dtype=torch.float32)
label = torch.tensor(self.label[index].values, dtype=torch.float32)
odds_rate = torch.tensor(
self.odds_rate[index].values, dtype=torch.float32)
mask = torch.ones_like(label).masked_fill(label == 19, 0)
return {
"num_feas": num_feas,
"cat_feas": cat_feas,
"label": label,
"odds_rate": odds_rate,
"mask": mask
}
実際にパディングされているか確認
idf = dataset.train
tensor_dataset = CustomKaibaAIDatasetForMultiTask(idf, num_feas, cat_feas)
from torch.utils.data import DataLoader
data_loader = DataLoader(tensor_dataset, batch_size=10, shuffle=False)
datas = next(iter(data_loader))
print(datas["num_feas"][0])
分かりずらいけど、最後あたりの要素が全て0になっているのが分かる
全体のデータのシェイプを見てみる
print("shape: \t\t\t[batch_size, horse_num, features_size]")
print("num_feas shape: \t", datas["num_feas"].shape)
print("cat_feas shape: \t", datas["cat_feas"].shape)
print("label shape: \t\t", datas["label"].shape)
print("odds_rate shape: \t", datas["odds_rate"].shape)
ちゃんと(バッチサイズ、18馬立て、特徴量サイズ)のバッチ形式の2次元テンソルとなっている
よって、dataset_mappingにDatasetクラスを持たせる
for key, dataset in dataset_mapping.items():
dataset_mapping[key].train_dataset = CustomKaibaAIDatasetForMultiTask(
dataset.train, num_feas, cat_feas)
dataset_mapping[key].valid_dataset = CustomKaibaAIDatasetForMultiTask(
dataset.valid, num_feas, cat_feas)
dataset_mapping[key].test_dataset = CustomKaibaAIDatasetForMultiTask(
dataset.test, num_feas, cat_feas)
4.損失関数の作成¶
損失関数はKL情報量をベースにしています。
KL情報量については、以下の記事を参考にされてください。

損失関数の作成で注意すべきことは、かならずスカラー形式で出力することです。
理由の説明をすると長くなりますが、モデルのつながりを調整する計算をするには、スカラー量になっていないとうまく計算できないからとだけにとどめておきます。
さて、今回作成する損失関数は、二つのタスクのロスを計算します。
そのため、入力が4つあります。
- input1: 着順の予測結果
- input2: オッズの勝率分布の予測結果
- input3: 正解の着順
- input4: 最終オッズの勝率分布
上記に注意して、以下の3つのロスを計算します。
- loss1: 着順予測の結果(input1)から上位3件のオッズの勝率分布の予測結果(input2)と、正解の着順(input3)の上位3件の最終オッズの勝率分布のKL情報量損失
- loss2: オッズの勝率分布の回帰タスク
- loss3: 実際の着順(input3)と予測着順(input1)のペアワイズ損失
そして出力を以下とします。
$$
loss = \lambda_{1} \times loss1 + \lambda_{2} \times loss2 + \lambda_{3} \times loss3
$$
つまり、オッズの推定と上位3件のオッズの分布の一致度の改善をloss1が担っており、全体の着順の予測結果の改善をloss2で管理しています。
そのため、上位3件のオッズが一致するように学習しながらオッズの分布推定をするタスクと着順のランキング学習を行うタスクの2つを学習するようになっています
import torch.nn as nn
if 1:
class MultiTaskLoss(nn.Module):
def __init__(self, l1=1/3, l2=1/3, l3=1/3, topn=1):
super(MultiTaskLoss, self).__init__()
self.l1 = l1
self.l2 = l2
self.l3 = l3
self.topn = topn
self.KLloss1 = nn.KLDivLoss(reduction="batchmean")
self.KLloss2 = nn.KLDivLoss(reduction="batchmean")
# self.MAE = nn.MSELoss()
self.MAE = nn.L1Loss()
self.loss1 = 0
self.loss2 = 0
self.loss3 = 0
def forward(self, pred1: torch.Tensor, pred2: torch.Tensor, label: torch.Tensor, odds_rate: torch.Tensor, mask: torch.Tensor) -> torch.Tensor:
if len(pred1.shape) == 1:
batch_size = 1
pred1, pred2, label, odds_rate, mask = pred1.unsqueeze(0), pred2.unsqueeze(
0), label.unsqueeze(0), odds_rate.unsqueeze(0), mask.unsqueeze(0)
else:
batch_size = pred1.shape[0]
# loss1
_, indices = torch.topk(label, k=self.topn, largest=False)
_, indices2 = torch.topk(label, k=18-self.topn)
ans_proba = torch.cat([torch.gather(odds_rate, dim=1, index=indices), torch.gather(
odds_rate, dim=1, index=indices2).sum(dim=1).reshape(batch_size, 1)], dim=1)
_, indices_pred1 = torch.topk(pred1, k=self.topn)
_, indices_pred2 = torch.topk(pred1, k=18-self.topn, largest=False)
pred_proba = torch.cat([torch.gather(pred2, dim=1, index=indices_pred1), torch.gather(
pred2, dim=1, index=indices_pred2).sum(dim=1).reshape(batch_size, 1)], dim=1)
loss1 = self.KLloss1(nn.functional.log_softmax(
pred_proba, dim=1), ans_proba)
self.loss1 = loss1.item()
# loss2
# loss2 = self.KLloss2(self.log_softmax(pred2), odds_rate)
# loss2 = self.MAE(
# nn.functional.softmax(pred2, dim=1), odds_rate)
# pred2 = 0.8/torch.clip(nn.functional.softmax(pred2, dim=1), 0.8/500)
# odds_rate = 0.8/torch.clip(odds_rate, 0.8/500)
pred2 = torch.log(torch.clip(
nn.functional.softmax(pred2, dim=1), 0.8/500))
odds_rate = torch.log(torch.clip(odds_rate, 0.8/500))
loss2 = self.MAE(pred2, odds_rate)
self.loss2 = loss2.item()
# loss3
ans_rank = (19 - label)
pair_diff = pred1.unsqueeze(2) - pred1.unsqueeze(1)
# pair_labels = (ans_rank.unsqueeze(2) - ans_rank.unsqueeze(1)).sign()
pair_labels = 5*(ans_rank.unsqueeze(2) - ans_rank.unsqueeze(1))
# 数値安定性を考慮したロジスティック損失
log_loss = nn.functional.softplus(-pair_labels * pair_diff)
# 平均損失を返す
loss3 = log_loss.mean()
self.loss3 = loss3.item()
# loss3 = self.KLloss2(
# nn.functional.log_softmax(pred2, dim=1), odds_rate)
return self.l1*loss1 + self.l2*loss2 + self.l3*loss3
# return self.l2*log_loss + self.l3*loss3
適当にロスの計算がどうなるか確認してみる
datas1 = dataset_mapping["2019first"].valid_dataset[0]
datas1["label"], datas1["odds_rate"]
ダミーデータの作成
# 着順予測:スコア値、確信度的なものなので、適当に正規分布からランダムサンプリング
output1 = torch.cat([torch.randn_like(datas1["odds_rate"][datas1["label"] < 19]),
torch.zeros_like(datas1["label"][datas1["label"] >= 19])])
# オッズの勝率分布推定:パディングを除いて正規化された確率値なので、すべて1にしてsoftmaxで正規化する。つまりすべてのオッズ値が等しい状態にする
output2 = torch.cat([torch.log_softmax(torch.ones_like(datas1["odds_rate"][datas1["label"] < 19]), dim=0),
torch.zeros_like(datas1["label"][datas1["label"] >= 19])-100])
# 微分可能かの確認用に勾配計算の対象とする
output1 = torch.tensor(output1, requires_grad=True)
output2 = torch.tensor(output2, requires_grad=True)
output1, output2
ロスの計算
criterion = MultiTaskLoss(topn=17)
loss = criterion(output1, output2,
datas1["label"], datas1["odds_rate"], datas1["mask"])
loss.backward(retain_graph=True) # 微分計算
loss
なんとなくそれっぽい損失が出てるのでOKとする
微分計算が出来ているか確認
output1.grad, output2.grad
パディングしたとこも微分計算されてるけど、まあ一旦見なかったことにします。
5.PyTorchによる最適な買い目を選択する深層学習モデルの作成¶
オッズの勝率分布の推定と着順の予測を同時に行うモデルを作ります
import math
from typing import Literal
import torch.nn.functional as F
class KeibaAIThirdModelForMultiTask(nn.Module):
def __init__(self, cat_num_list: list[int], numerous_feature_num: int) -> None:
super(KeibaAIThirdModelForMultiTask, self).__init__()
cat_embed_list = []
self.embed_num_list = []
for cat_num in cat_num_list:
embed_num = round(math.sqrt(cat_num))
self.embed_num_list += [embed_num]
embed_layer = nn.Embedding(
cat_num, embed_num, padding_idx=cat_num-1)
cat_embed_list += [embed_layer]
# カテゴリのベクトル埋め込み用レイヤー
self.cat_embed_list = nn.ModuleList(cat_embed_list)
self.cat_num_list = cat_num_list
# 畳み込み層
self.conv1 = nn.Conv2d(
in_channels=1, out_channels=8, kernel_size=3, stride=1, padding=1)
# 畳み込み層(共有)
self.shared_conv = nn.Conv2d(
in_channels=8, out_channels=8, kernel_size=3, stride=1, padding=1)
self.task1_input0 = nn.Linear(
8 * (18//4) * (((numerous_feature_num+sum(self.embed_num_list))//2)//2), 2048)
self.task2_input0 = nn.Linear(
8 * (18//4) * (((numerous_feature_num+sum(self.embed_num_list))//2)//2), 2048)
self.task1_input1 = nn.Linear(2048, 512)
self.task2_input1 = nn.Linear(2048, 512)
self.task1_input2 = nn.Linear(512, 256)
self.task2_input2 = nn.Linear(512, 256)
self.task1_input3 = nn.Linear(256, 128)
self.task2_input3 = nn.Linear(256, 128)
self.task1_input4 = nn.Linear(128, 64)
self.task2_input4 = nn.Linear(128, 64)
# タスク1: 着順の推定
self.fc_task1 = nn.Linear(64, 18)
# タスク2: オッズの分布推定
self.fc_task2 = nn.Linear(64, 18)
self.drop_rate = 0.25
self.dropout = nn.Dropout(p=self.drop_rate)
self.relu = nn.ReLU()
# self.log_softmax = nn.LogSoftmax(dim=0)
self.mode = torch.tensor(0)
self.max_pool1 = nn.MaxPool2d(kernel_size=2, stride=2)
self.max_pool2 = nn.MaxPool2d(kernel_size=2, stride=2)
def forward(self, x_num: torch.Tensor, x_cat_list: torch.Tensor) -> torch.Tensor:
x_cat_list = x_cat_list.int()
cat_embed_list = [self.cat_embed_list[idx](
x_cat.T) for idx, x_cat in enumerate(x_cat_list.T)]
cat_embed_list = torch.cat(
cat_embed_list, dim=2 if len(x_cat_list.shape) > 2 else 1)
x = torch.cat([x_num, cat_embed_list],
dim=2 if len(x_num.shape) > 2 else 1).unsqueeze(1 if len(x_num.shape) > 2 else 0)
# 畳み込み層 + プーリング
# input(batch_size, 1, 18, 特徴量数) -> (batch_size, 16, 18, 特徴量数)
x = self.relu(self.conv1(x))
# (batch_size, 16, 18, 特徴量数) -> (batch_size, 16, 9, 特徴量数//2)
x = self.max_pool1(x)
# 畳み込み層(共有)
# (batch_size, 16, 9, 特徴量数//2) -> (batch_size, 32, 9, 特徴量数//2)
x = self.relu(self.shared_conv(x))
# (batch_size, 32, 9, 特徴量数//2) -> (batch_size, 32, 4, 特徴量数//4)
x = self.max_pool2(x)
# フラット化
if len(x_num.shape) > 2:
x = x.view(x.size(0), -1)
else:
x = x.view(-1)
# タスク1: 着順の推定
x_task1 = self.dropout(self.relu(self.task1_input0(x)))
x_task1 = self.dropout(self.relu(self.task1_input1(x_task1)))
x_task1 = self.dropout(self.relu(self.task1_input2(x_task1)))
x_task1 = self.dropout(self.relu(self.task1_input3(x_task1)))
x_task1 = self.dropout(self.relu(self.task1_input4(x_task1)))
task1_output: torch.Tensor = self.fc_task1(x_task1)
# タスク2: オッズの分布推定
x_task2 = self.dropout(self.relu(self.task2_input0(x)))
x_task2 = self.dropout(self.relu(self.task2_input1(x_task2)))
x_task2 = self.dropout(self.relu(self.task2_input2(x_task2)))
x_task2 = self.dropout(self.relu(self.task2_input3(x_task2)))
x_task2 = self.dropout(self.relu(self.task2_input4(x_task2)))
task2_output: torch.Tensor = self.fc_task2(x_task2)
# task2_output = self.log_softmax(task2_output)
if self.mode < 1:
return task1_output, task2_output
elif self.mode < 2:
return task1_output
else:
return task2_output
def predict(self, x_num: torch.Tensor, x_cat_list: torch.Tensor, mask: torch.Tensor) -> torch.Tensor:
output1, output2 = self.forward(x_num, x_cat_list)
return output1[mask > 0], output2[mask > 0]
from torchviz import make_dot # type: ignore
from torch.utils.data import DataLoader # type: ignore
dataset = dataset_mapping["2019first"]
dataset_loader = DataLoader(dataset.train_dataset, batch_size=1, shuffle=True)
datas1 = next(iter(dataset_loader))
model = KeibaAIThirdModelForMultiTask(dataset.cat_num_list, len(num_feas))
model.eval()
y = model(datas1["num_feas"][0], datas1["cat_feas"][0])
dot = make_dot(y, params=dict(model.named_parameters()))
# SVG形式でモデル構造の出力
dot.render('KeibaAIThirdModelForMultiTask_Graph', format="svg")
y
今回からLightGBMの時と同様にEarly Stoppingを採用する
これを導入することで、学習データに過学習する前に検証データのロスが悪化した段階で学習をやめるようになります。
Early Stopの実装方法は調べればいくらでも出てきますが、今回はオプティマイザの学習率と連動させることで、より効果的なEarly Stoppingの機能を実装してみました。
# Early Stopping クラス
class EarlyStopping:
def __init__(self, patience=5, min_delta=0.0, lr_threshold=1e-9, path='best_model.pth'):
"""
patience: 改善が見られないエポック数の許容値
min_delta: 改善とみなす最小の変化量
path: 最良モデルを保存するファイルパス
"""
self.patience = patience
self.min_delta = min_delta
self.counter = 0
self.best_loss = float('inf')
self.early_stop = False
self.path = path
self.lr_threshold = lr_threshold
self.best_epoch = 0
def __call__(self, val_loss, model, epoch, current_lr):
# 学習率が閾値を下回った場合、Early Stoppingを有効化
if current_lr <= self.lr_threshold:
print(
f"Learning rate ({current_lr:.2e}) is below the threshold ({self.lr_threshold:.2e}). Stopping training.")
self.early_stop = True
return
if self.best_loss is None or val_loss < self.best_loss - self.min_delta:
# 改善が見られた場合、モデルを保存
self.best_loss = val_loss
self.counter = 0
torch.save(model.state_dict(), self.path) # 最良モデルを保存
self.best_epoch = epoch+1
else:
self.counter += 1
if self.counter >= self.patience:
self.early_stop = True
def load_best_model(self, model, device):
"""保存した最良モデルをロードする"""
model.load_state_dict(torch.load(self.path, map_location=device))
6.学習の実行¶
PyTorchの関係上、Seed値を固定してても学習結果にブレが生じてしまいます。(ここが深層学習モデルのちょっと嫌なところ)
そのため、ここではモデルを20個ぐらい作って最も良いモデルを選ぼうという手段を取ってます。
また、今回は学習・検証・テストを以下のデータにしています。
- 学習: 2022年12月31日以前のレース結果
- 検証: 2023年1月1日から2023年6月30日までのレース結果
- テスト: 2023年7月1日から2023年12月31日までのレース結果
import tqdm
import numpy as np
from torch.utils.tensorboard import SummaryWriter
import datetime
for _ in range(20):
del model
torch.cuda.empty_cache()
# チュートリアルなので、dataset_mappingの内ひとつだけのdatasetを対象にモデルを学習してみる
target_dataset = dataset_mapping["2023second"]
# デバイスの設定(GPUが利用可能な場合)
device = torch.device('cuda:0' if torch.cuda.is_available() else 'cpu')
# device = "cpu"
# モデルの初期化
model = KeibaAIThirdModelForMultiTask(
target_dataset.cat_num_list, len(num_feas)).to(device)
# 損失関数
param = np.array([1., 1., 1.])
param /= param.sum()
loss_fn = MultiTaskLoss(*param.tolist(), topn=3)
# オプティマイザ
optimizer = torch.optim.AdamW(
model.parameters(), lr=5e-4, weight_decay=0.5)
# スケジューラー (ReduceLROnPlateau)
scheduler = torch.optim.lr_scheduler.ReduceLROnPlateau(
optimizer, mode='min', factor=0.5, patience=2, verbose=True)
# Early Stopping インスタンス
best_model_path = "runs/third_model_monitor/" + \
datetime.datetime.now().strftime("%Y%m%d-%H%M%S")
early_stopping = EarlyStopping(
patience=10, min_delta=0.0000, lr_threshold=1e-7, path=best_model_path+"/best_model.pth")
# 1.DataLoaderの作成
train_dataloader = DataLoader(
target_dataset.train_dataset, batch_size=1024, shuffle=True)
valid_dataloader = DataLoader(target_dataset.valid_dataset, batch_size=len(
target_dataset.valid_dataset), shuffle=False)
test_dataloader = DataLoader(
target_dataset.test_dataset, batch_size=len(target_dataset.test_dataset), shuffle=False)
writer = SummaryWriter(log_dir=best_model_path)
loss_list_all = []
# 学習ループ
num_epochs = 100
valid_loss, test_loss, best_loss, global_step = 0, 0, 0, 0
torch.cuda.empty_cache()
with tqdm.tqdm(total=len(train_dataloader)*num_epochs, desc=f"Epoch 1/{num_epochs}. loss: train=None, valid=None, test=None, Best=None (0)") as pbar:
for epoch in range(num_epochs):
model.train() # 訓練モード
loss_list = []
for datas in train_dataloader:
global_step += 1
num_data, cat_data_list, labels, odds_rate, mask = datas["num_feas"], datas[
"cat_feas"], datas["label"], datas["odds_rate"], datas["mask"]
# データとラベルをGPUに転送
num_data, cat_data_list, labels, odds_rate, mask = num_data.to(
device), cat_data_list.to(device), labels.to(device), odds_rate.to(device), mask.to(device)
# 順伝播
optimizer.zero_grad() # 勾配を初期化
outputs = model(num_data, cat_data_list)
# 損失の計算
loss = loss_fn(outputs[0], outputs[1], labels, odds_rate, mask)
# 逆伝播
loss.backward()
# 最適化
optimizer.step()
current_lr = optimizer.param_groups[0]['lr']
writer.add_scalar('Loss/Loss1 (TOPn オッズ分布)',
loss_fn.loss1, global_step)
writer.add_scalar('Loss/Loss2 (オッズ推定MAE)',
loss_fn.loss2, global_step)
writer.add_scalar('Loss/Loss3 (着順Pair Wise)',
loss_fn.loss3, global_step)
writer.add_scalar('Loss/Total', loss.item(), global_step)
# ロスを記録
loss_list += [loss.item()]
pbar.update()
pbar.set_description(
desc=f"Epoch {epoch+1}/{num_epochs}. loss: train={np.mean(loss_list):.4f}, valid={valid_loss:.4f}, test={test_loss:.4f}, Best={best_loss:.4f} ({early_stopping.best_epoch})")
del num_data, cat_data_list, labels, odds_rate, mask, datas
loss_list_all += [loss_list]
model.eval() # 推論モード
with torch.no_grad():
# 検証データのロス確認
for datas in valid_dataloader:
num_data, cat_data_list, labels, odds_rate, mask = datas["num_feas"], datas[
"cat_feas"], datas["label"], datas["odds_rate"], datas["mask"]
# データとラベルをGPUに転送
num_data, cat_data_list, labels, odds_rate, mask = num_data.to(
device), cat_data_list.to(device), labels.to(device), odds_rate.to(device), mask.to(device)
# 順伝播
outputs = model(num_data, cat_data_list)
# 損失の計算
loss = loss_fn(outputs[0], outputs[1],
labels, odds_rate, mask)
del num_data, cat_data_list, labels, odds_rate, mask, datas
# テストデータのロス確認
for datas in test_dataloader:
num_data, cat_data_list, labels, odds_rate, mask = datas["num_feas"], datas[
"cat_feas"], datas["label"], datas["odds_rate"], datas["mask"]
# データとラベルをGPUに転送
num_data, cat_data_list, labels, odds_rate, mask = num_data.to(
device), cat_data_list.to(device), labels.to(device), odds_rate.to(device), mask.to(device)
# 順伝播
outputs_test = model(num_data, cat_data_list)
# 損失の計算
loss_test = loss_fn(
outputs_test[0], outputs_test[1], labels, odds_rate, mask)
del num_data, cat_data_list, labels, odds_rate, mask, datas
valid_loss = loss.item()
test_loss = loss_test.item()
writer.add_scalar('Epoch Loss/Total-Train',
np.mean(loss_list), global_step)
writer.add_scalar('Epoch Loss/Total-Valid',
valid_loss, global_step)
writer.add_scalar('Epoch Loss/Total-Test',
test_loss, global_step)
# 学習率スケジューラーの更新
scheduler.step(valid_loss, epoch)
writer.add_scalar('Learning Rate/current', current_lr, epoch)
# Early Stopping のチェック
early_stopping(valid_loss, model, epoch, current_lr)
best_loss = early_stopping.best_loss
pbar.set_description(
desc=f"Epoch {epoch+1}/{num_epochs}. loss: train={np.mean(loss_list):.4f}, valid={valid_loss:.4f}, test={test_loss:.4f}, Best={best_loss:.4f} ({early_stopping.best_epoch})")
if early_stopping.early_stop:
print(f"Early stopping at epoch {epoch+1}")
break
torch.cuda.empty_cache()
writer.close()
# 最良モデルに戻す
early_stopping.load_best_model(model, device)
print(
f"Restored the best model parameters! Best Epoch: {early_stopping.best_epoch}, Best Loss: {early_stopping.best_loss}")
torch.cuda.empty_cache()
7.分析¶
学習した20個のモデルから、推論済データを作成する。
結構面倒だが、モデル作成時に推論用のメソッドを用意してるので、それを活用している
import tqdm
import numpy as np
target_dataset = dataset_mapping["2023second"]
device = torch.device('cuda:0' if torch.cuda.is_available() else 'cpu')
dataMap = {}
root_model_dir = pathlib.Path("./runs/third_model_monitor")
for path in tqdm.tqdm(list(root_model_dir.glob("**/*.pth"))):
# モデルの初期化
model = KeibaAIThirdModelForMultiTask(
target_dataset.cat_num_list, len(num_feas)).to(device)
model.load_state_dict(torch.load(path, map_location=device))
with torch.no_grad():
model.to(device)
model.eval()
train_dataloader = DataLoader(
target_dataset.train_dataset, batch_size=1024, shuffle=False)
valid_dataloader = DataLoader(target_dataset.valid_dataset, batch_size=len(
target_dataset.valid_dataset), shuffle=False)
test_dataloader = DataLoader(
target_dataset.test_dataset, batch_size=len(target_dataset.test_dataset), shuffle=False)
all_outputs0 = []
all_outputs1 = []
for datas in train_dataloader:
num_data, cat_data_list, labels, odds_rate, mask = datas["num_feas"], datas[
"cat_feas"], datas["label"], datas["odds_rate"], datas["mask"]
# データとラベルをGPUに転送
num_data, cat_data_list, labels, odds_rate, mask = num_data.to(
device), cat_data_list.to(device), labels.to(device), odds_rate.to(device), mask.to(device)
# 順伝播
outputs = model.predict(num_data, cat_data_list, mask)
all_outputs0 += outputs[0].to("cpu").detach().numpy().tolist()
all_outputs1 += outputs[1].to("cpu").detach().numpy().tolist()
del num_data, cat_data_list, labels, odds_rate, mask
dftrain = target_dataset.train.copy()
dftrain["pred_odds_rate"] = np.exp(np.array(all_outputs1))
dftrain["pred_odds_rate"] /= dftrain["raceId"].map(
dftrain[["raceId", "pred_odds_rate"]].groupby("raceId")["pred_odds_rate"].sum())
dftrain["pred_odds"] = 0.8/dftrain["pred_odds_rate"]
dftrain["pred_odds_rank"] = dftrain.groupby(
"raceId")["pred_odds_rate"].rank(ascending=False).astype(int)
dftrain["pred_proba"] = np.array(all_outputs0)
dftrain["pred_rank"] = dftrain.groupby(
"raceId")["pred_proba"].rank(ascending=False).astype(int)
del all_outputs0, all_outputs1
for datas in valid_dataloader:
num_data, cat_data_list, labels, odds_rate, mask = datas["num_feas"], datas[
"cat_feas"], datas["label"], datas["odds_rate"], datas["mask"]
# データとラベルをGPUに転送
num_data, cat_data_list, labels, odds_rate, mask = num_data.to(
device), cat_data_list.to(device), labels.to(device), odds_rate.to(device), mask.to(device)
# 順伝播
outputs = model.predict(num_data, cat_data_list, mask)
del num_data, cat_data_list, labels, odds_rate, mask
dfvalid = target_dataset.valid.copy()
dfvalid["pred_odds_rate"] = np.exp(
outputs[1].to("cpu").detach().numpy())
dfvalid["pred_odds_rate"] /= dfvalid["raceId"].map(
dfvalid[["raceId", "pred_odds_rate"]].groupby("raceId")["pred_odds_rate"].sum())
dfvalid["pred_odds"] = 0.8/dfvalid["pred_odds_rate"]
dfvalid["pred_odds_rank"] = dfvalid.groupby(
"raceId")["pred_odds_rate"].rank(ascending=False).astype(int)
dfvalid["pred_proba"] = outputs[0].to("cpu").detach().numpy()
dfvalid["pred_rank"] = dfvalid.groupby(
"raceId")["pred_proba"].rank(ascending=False).astype(int)
del outputs
for datas in test_dataloader:
num_data, cat_data_list, labels, odds_rate, mask = datas["num_feas"], datas[
"cat_feas"], datas["label"], datas["odds_rate"], datas["mask"]
# データとラベルをGPUに転送
num_data, cat_data_list, labels, odds_rate, mask = num_data.to(
device), cat_data_list.to(device), labels.to(device), odds_rate.to(device), mask.to(device)
# 順伝播
outputs_test = model.predict(num_data, cat_data_list, mask)
del num_data, cat_data_list, labels, odds_rate, mask
dftest = target_dataset.test.copy()
dftest["pred_odds_rate"] = np.exp(
outputs_test[1].to("cpu").detach().numpy())
dftest["pred_odds_rate"] /= dftest["raceId"].map(
dftest[["raceId", "pred_odds_rate"]].groupby("raceId")["pred_odds_rate"].sum())
dftest["pred_odds"] = 0.8/dftest["pred_odds_rate"]
dftest["pred_odds_rank"] = dftest.groupby(
"raceId")["pred_odds_rate"].rank(ascending=False).astype(int)
dftest["pred_proba"] = outputs_test[0].to("cpu").detach().numpy()
dftest["pred_rank"] = dftest.groupby(
"raceId")["pred_proba"].rank(ascending=False).astype(int)
del outputs_test
del model
torch.cuda.empty_cache()
dataMap[path.parent.name] = {
"train": dftrain,
"valid": dfvalid,
"test": dftest
}
色々と工夫した結果、以下のようなフィルタリングを行うこととする。
フィルタリングとは、特定の条件に当てはまる馬券のみを選択する的なこと
代表的な例としては、確信度が0.5超えたものを対象にするなど、何かしらの数値に閾値を設けてルールベースで意思決定を下すこととなる
あまりこだわりすぎると泥沼になるので、一つの目安とする程度に留めておかないと実際の運用と大きく乖離して使い物にならない場合も起こり得るので注意すべきやり方です。
フィルタリング条件¶
今回のフィルタリングの条件を以下にしました
raceGrade: どのレースクラスからを対象にするか。0~8まで指定可能。- レースクラスとは?
raceGrade = 0のとき、新馬・未勝利戦以降のすべてのクラスを対象とするraceGrade = 1のとき、1勝クラス以降のすべてのクラスを対象とするraceGrade = 4のとき、オープンクラス以降のすべてのクラスを対象とするraceGrade = 6のとき、G3クラス以降のすべてのクラスを対象とする
cutRaceGrade: どのレースクラス以降を対象外にするか。
あまり使わないかも、泥沼の入り口になるのと重賞クラスを賭けないと面白くないので、9で固定しておくと良い
cutRaceGrade = 6のとき、重賞クラス以降のすべてのクラスを対象外とするcutFav: 予測オッズを元にした人気に対して、どこまでの人気を切り捨てるかを決めるパラメータ- たとえば、賭ける対象の予想人気が1番人気とかだと、高い的中率を求められるので対象から除外する場合とかに指定すると良い。穴馬狙いのAIを作りたいなら
cutFav=6とか指定する cutFav = 6のとき、予想人気が6番人気以下のものを対象外とする
- たとえば、賭ける対象の予想人気が1番人気とかだと、高い的中率を求められるので対象から除外する場合とかに指定すると良い。穴馬狙いのAIを作りたいなら
threash: 賭ける対象の予想オッズに対して、どこまでを許容するか。0~1.0を指定- 例えば、賭ける対象の予想オッズが100倍とかだと結構心許ないので、そういった高すぎるオッズをカットオフするためのパラメータ。だいたい0.95ぐらいが良いと思う。
backDays: 学習データの直近何日分を分析対象とするかthreashパラメータと関係があり、ここで指定した日数分を使って予想オッズの分布を割り出し、threashで使用する分位の分布を作ります。- だいたい過去5年とかそういった感じで使えばいいじゃないか?使用者の感覚にお任せします
betNum: 半年間の間で何回馬券を購入するかを指定するパラメータ- 常々思ってたことに、すべてのレースに賭けるのは現実的ではないよなという気持ちから、毎週10枚ペースで賭けるようなシミュレーションをしたいときに指定する
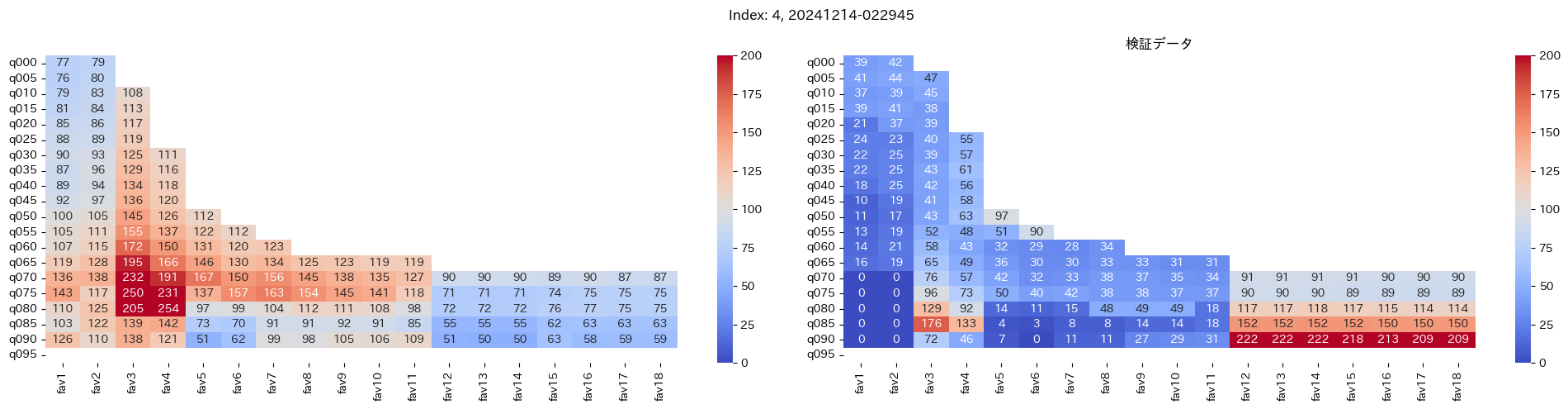
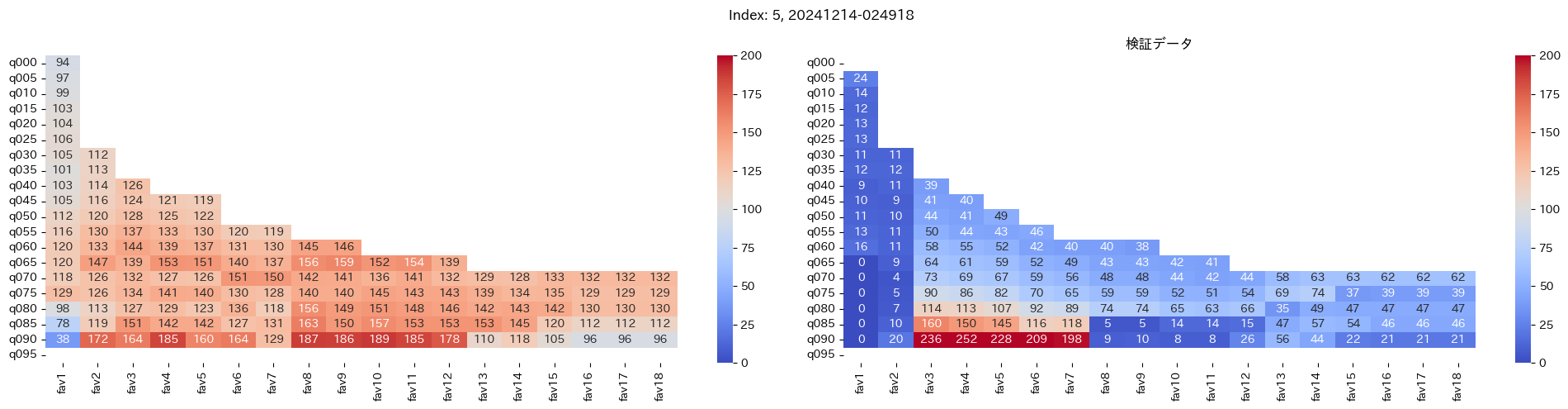
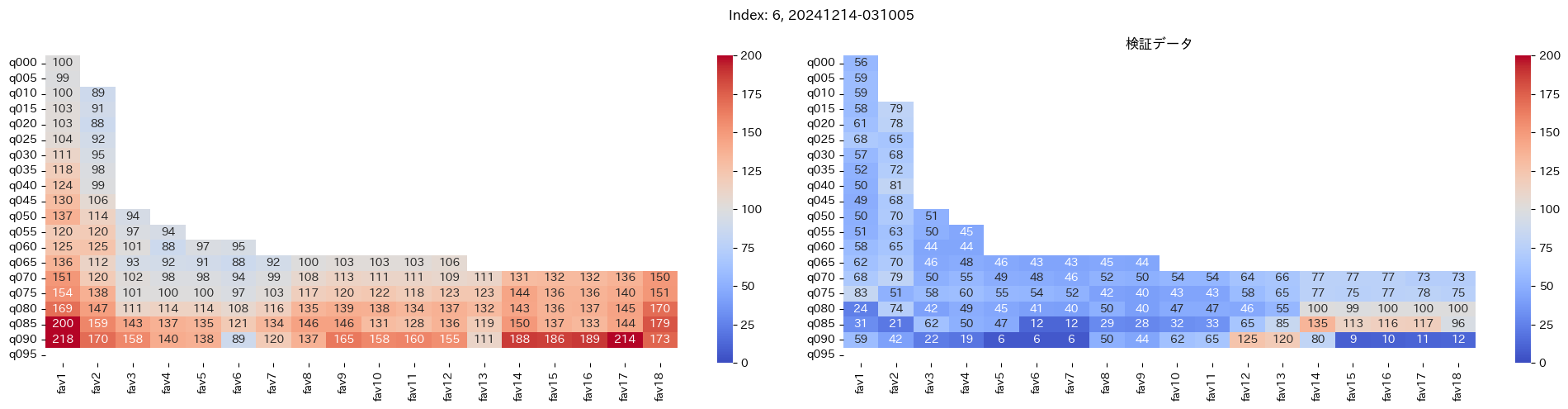
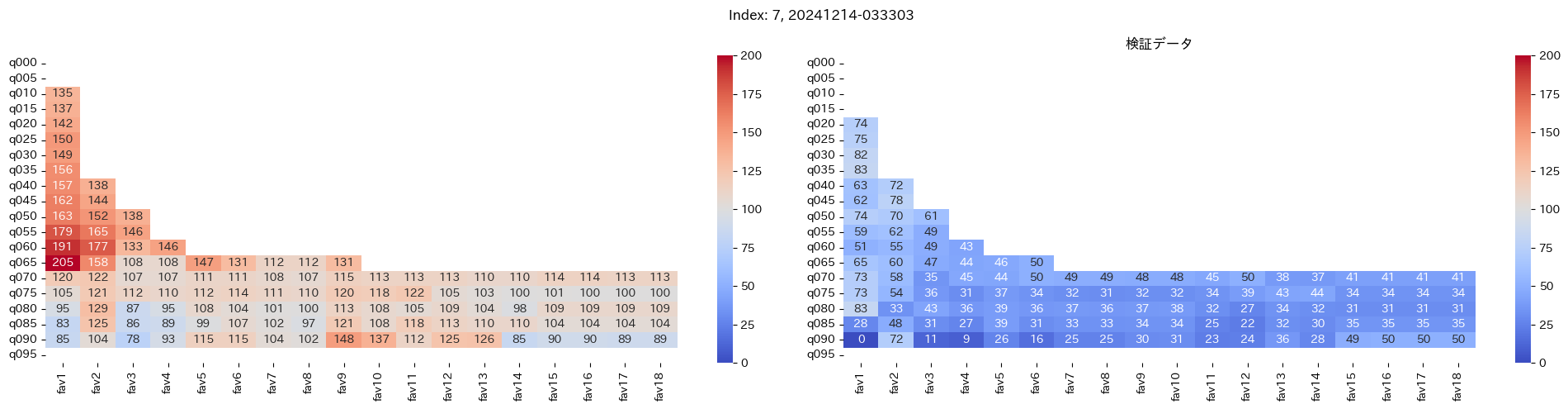
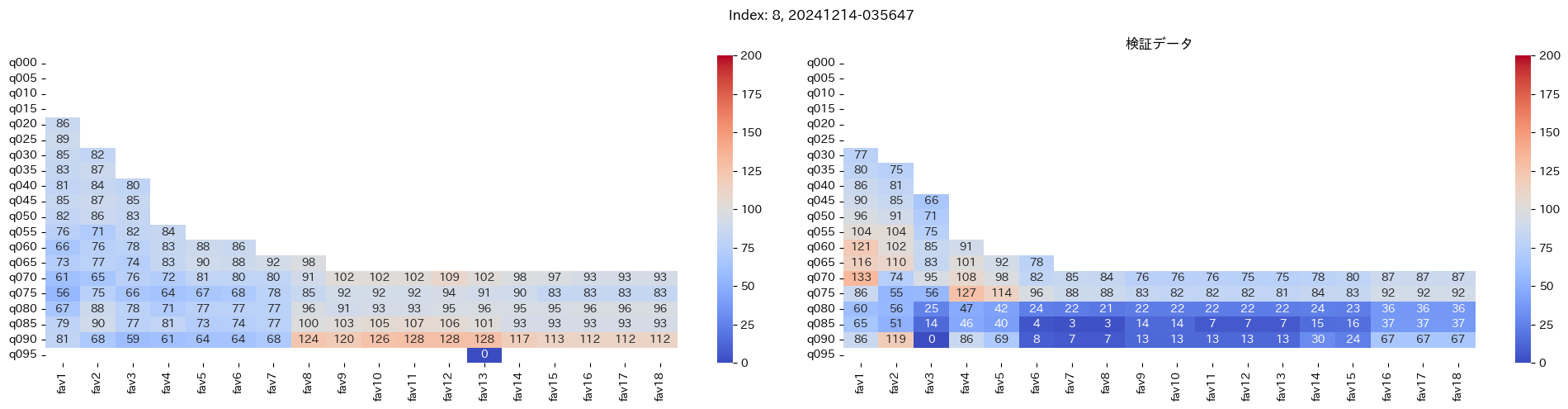
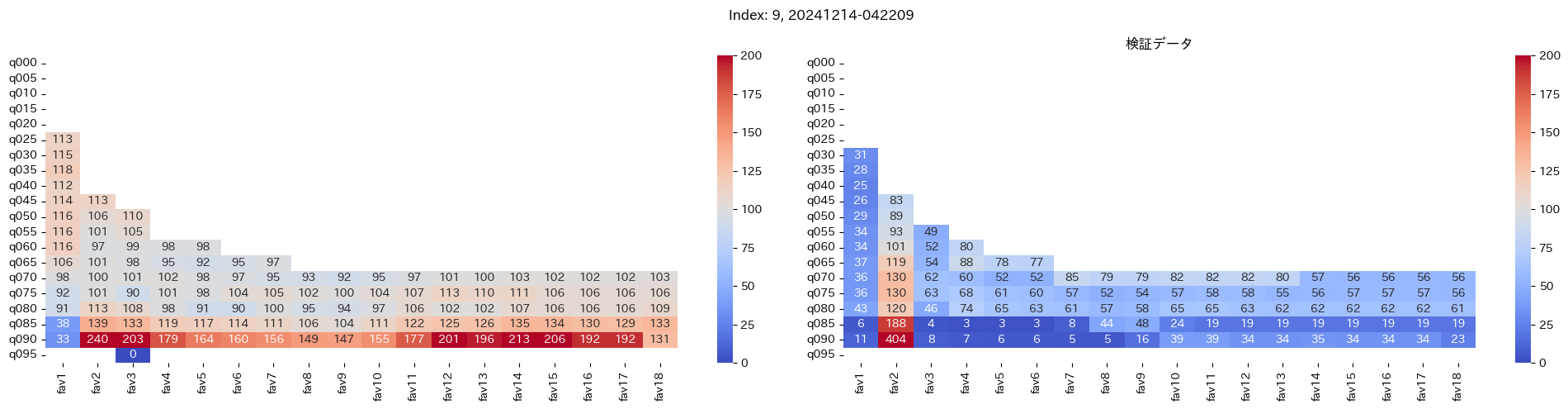
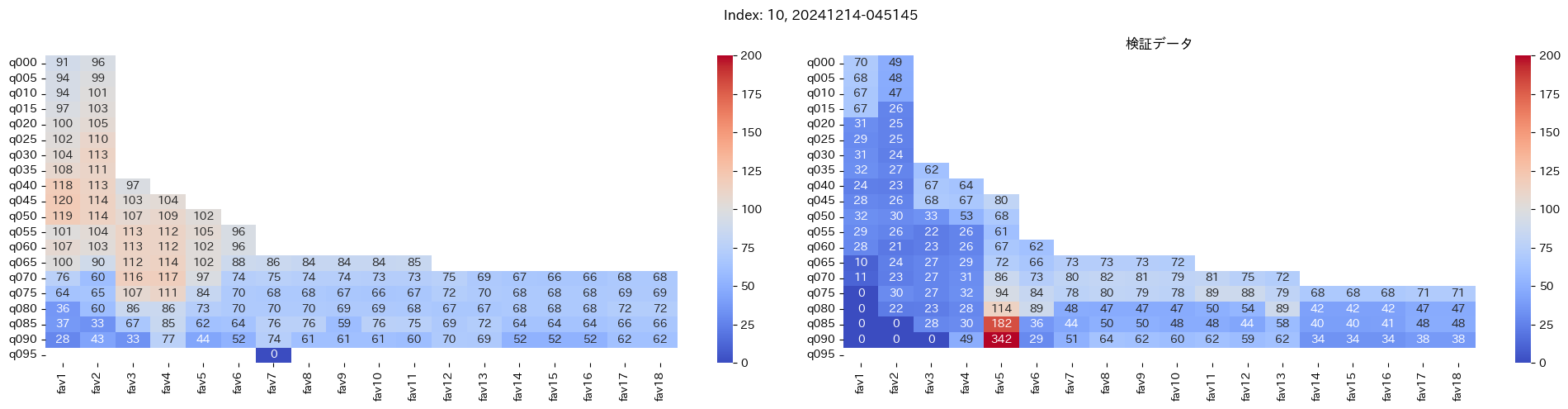
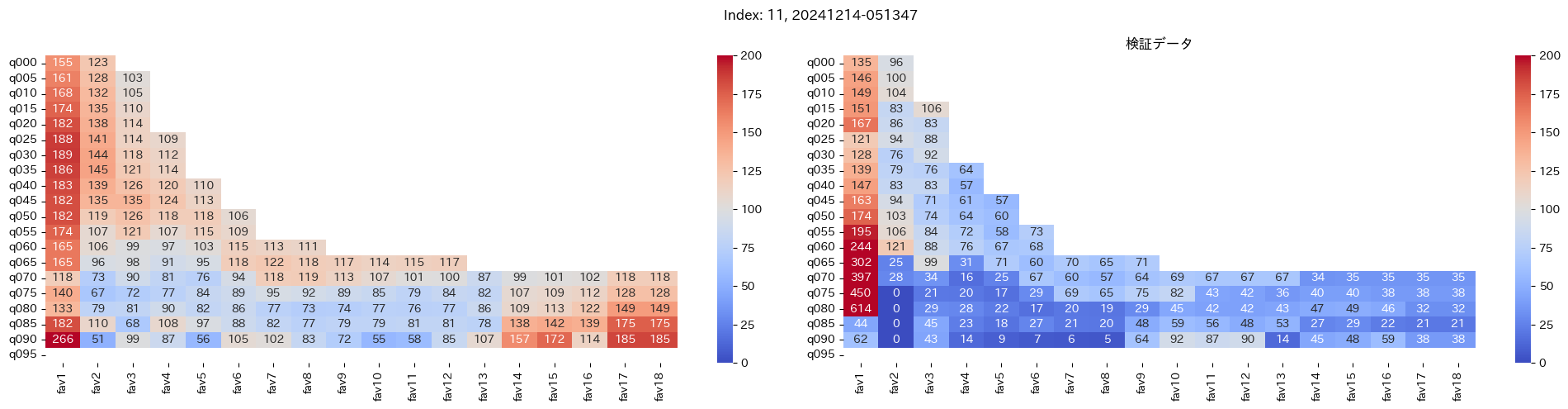
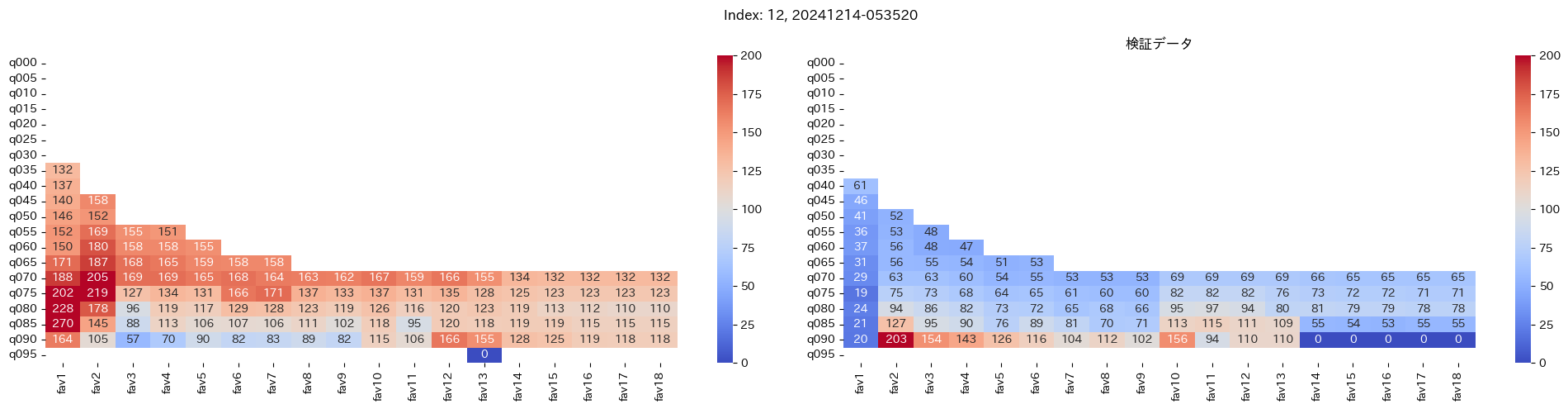
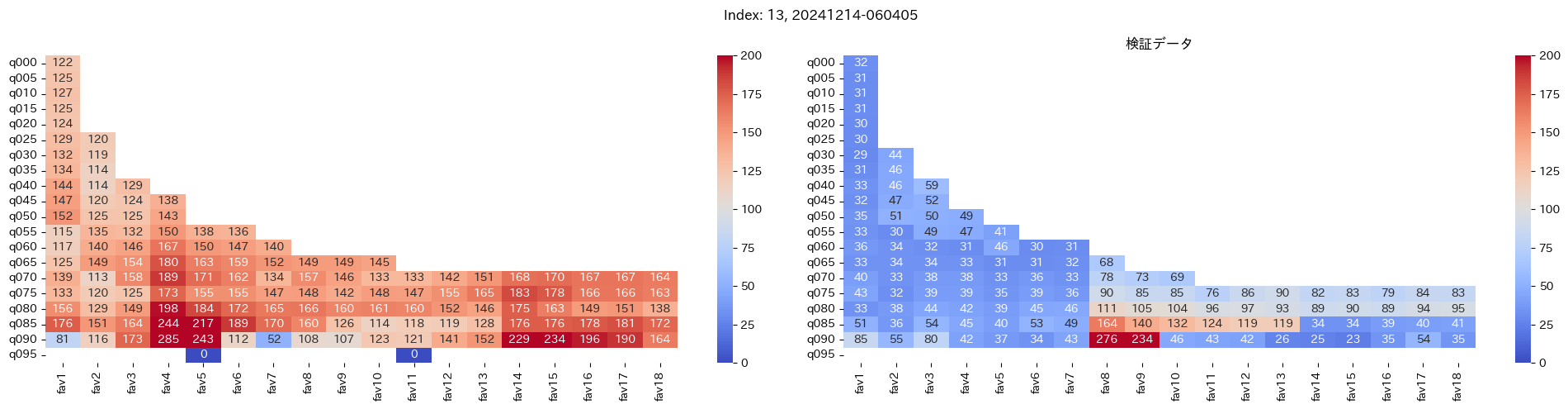
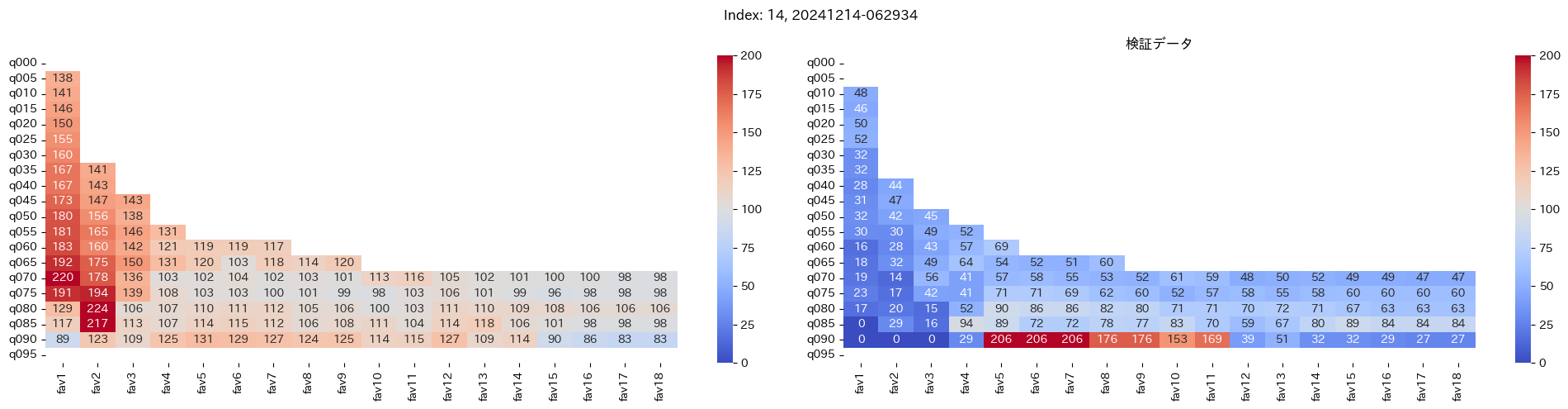
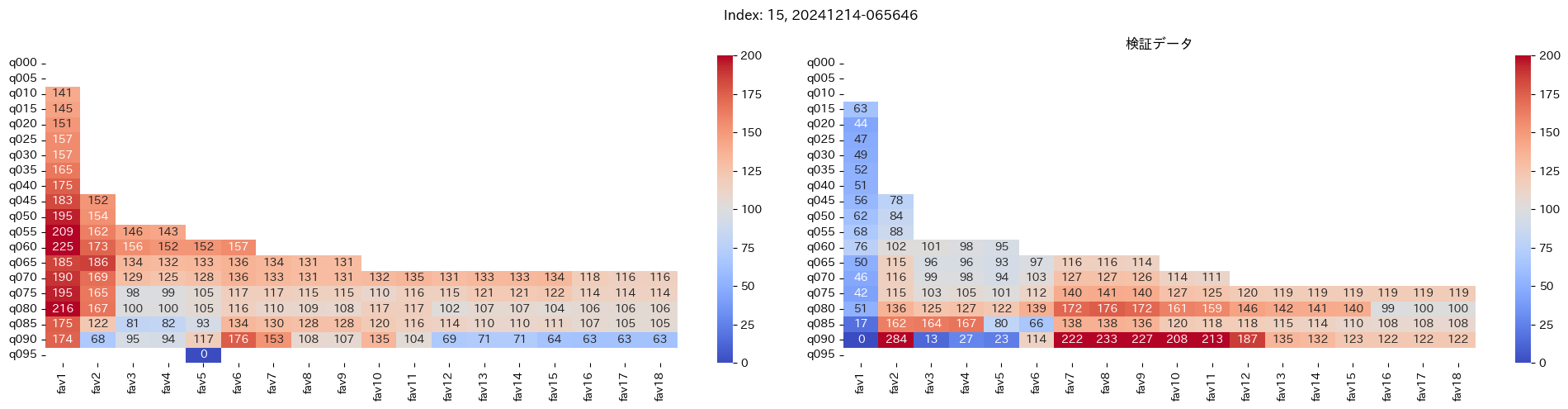
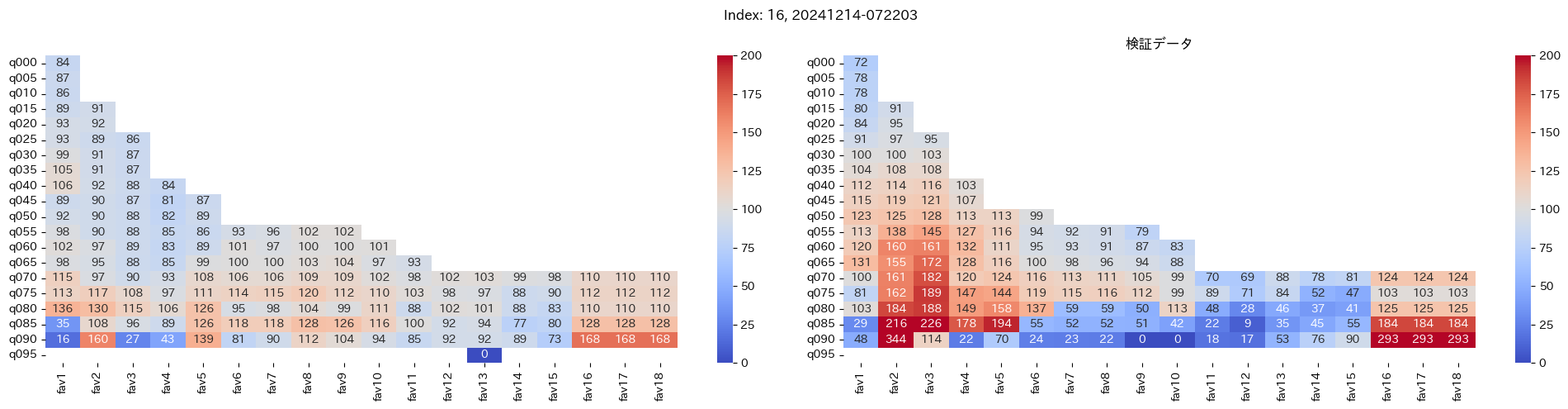
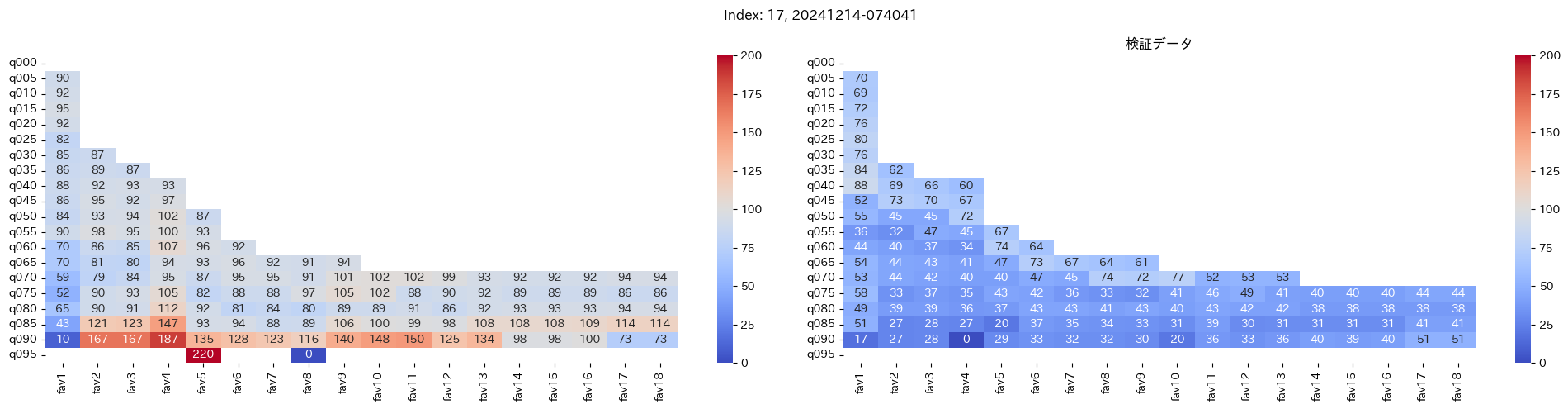
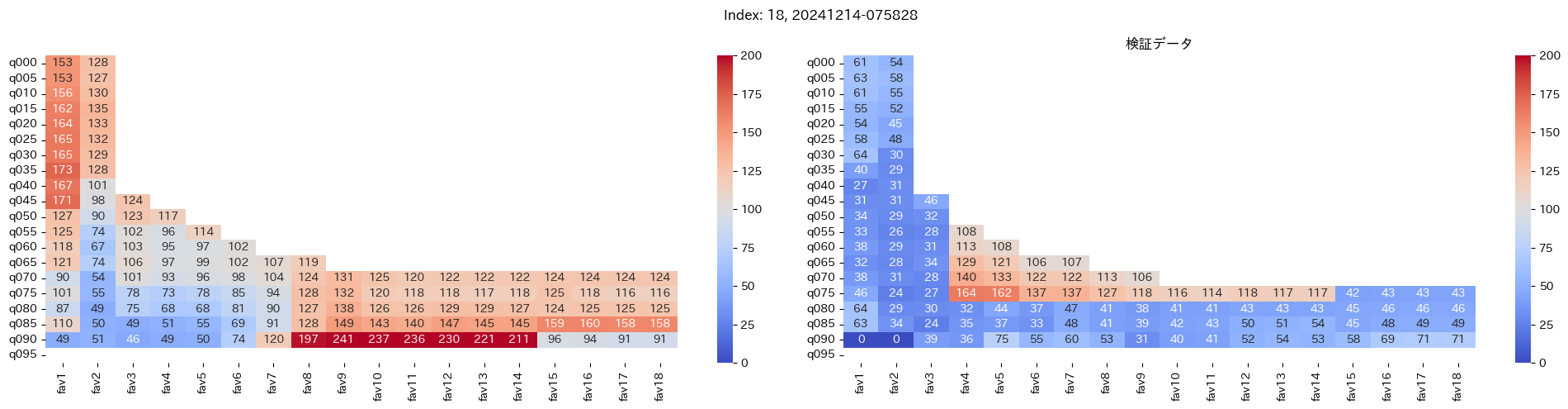
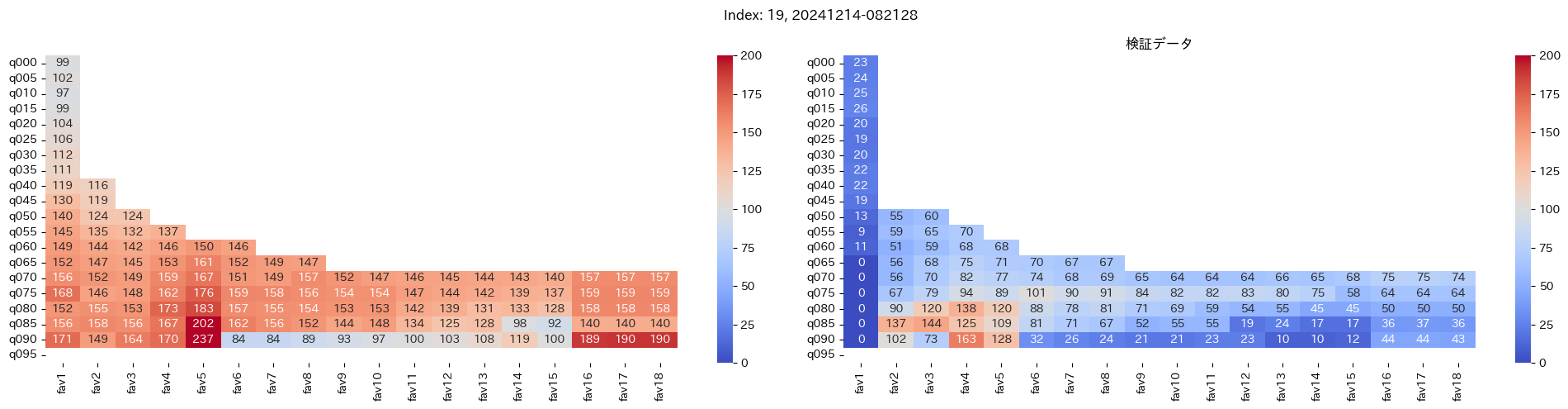
回収率マップの描画¶
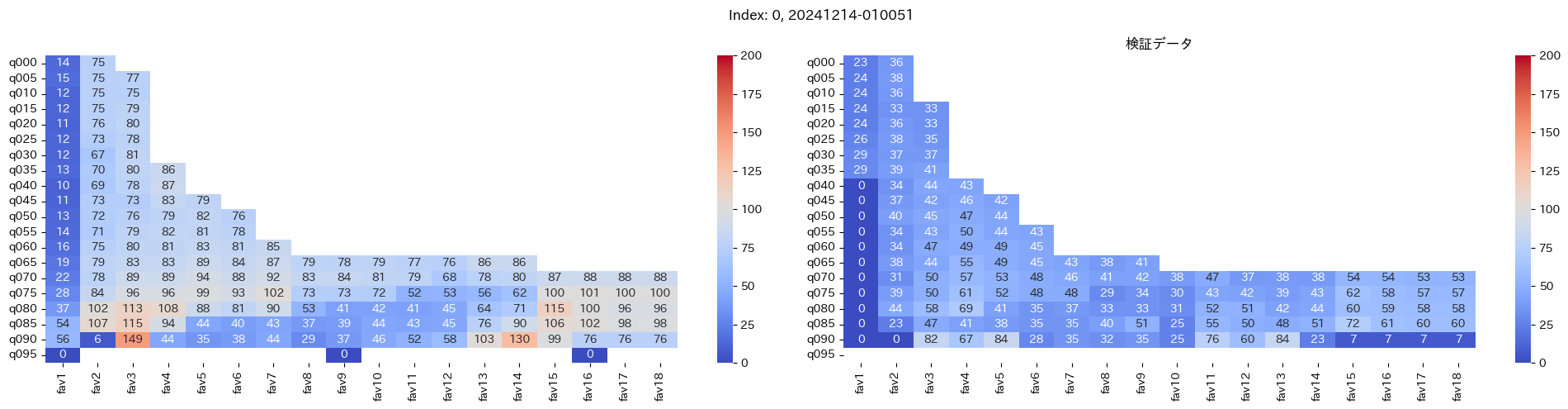
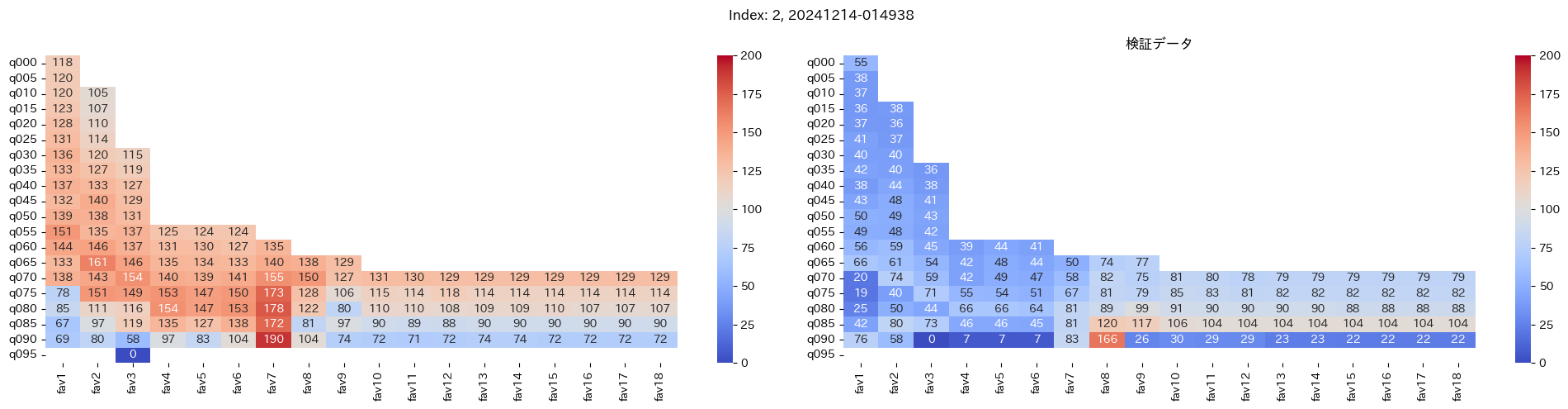
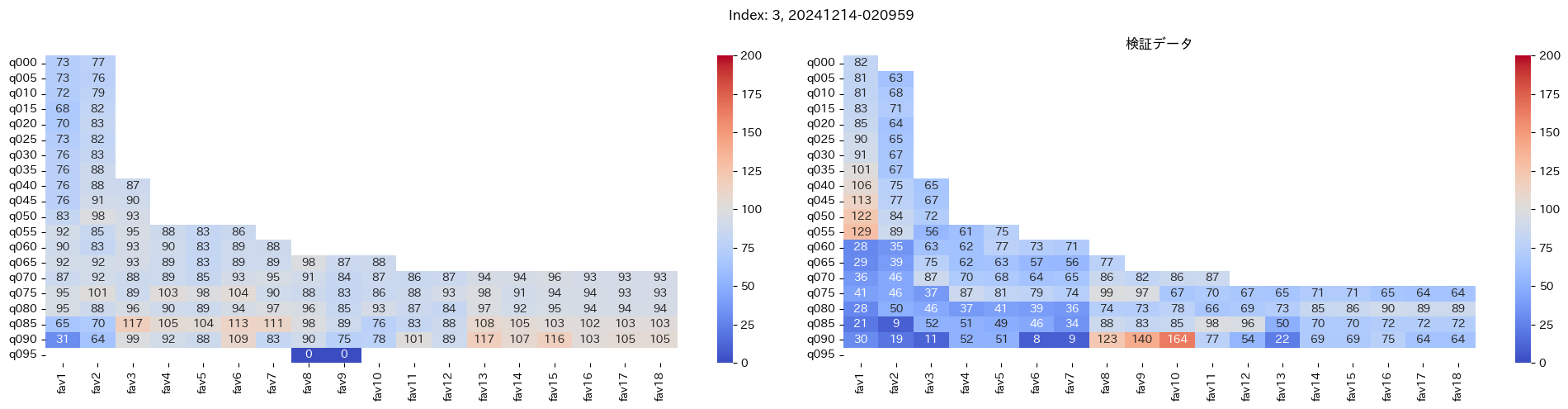
20モデル分のフィルタリングによる回収率マップを描画する
横軸に対象とする人気の範囲を上げていった場合の回収率分布を、縦軸に予想オッズを分位ごとに区切ったときの回収率分布を示しています。
つまり、横軸のfav18というのは、1番人気から18番人気までを対象とした場合の回収率分布になっています。(cutFav = 5など指定がある場合は、cutFavから18番人気までを対象とした回収率分布になります。)
縦軸の場合は、q020というのは、学習データを基にした予想オッズの20%分位から100%分位までを対象にした場合の回収率分布になります。(threash = 0.95と指定した場合は、20%分位からthreash分位までを対象にした回収率分布になります。)
描画結果は、階段状のヒートマップになっており、これはbetNumで指定した馬券購入枚数に基づいています。
例えば、betNum = 240と指定した場合に、ヒートマップの横軸fav18、縦軸q080に値があれば、
1番人気から18番人気までの範囲 かつ 予想オッズの80%分位からthreash分位までの範囲 を対象にしたときの馬券購入回数が240枚未満であることを示しており、そのマスに記載されている数字が回収率となっています。
import matplotlib.pyplot as plt
import japanize_matplotlib
import seaborn as sns
raceGrade, cutRaceGrade, cutFav = 1, 9, 0 # 1勝クラス以上のレースを対象に、含めないクラスの下限値
threash = .95
backDays = 365*5
betNum = 10*int(180/7) # 250枚: 毎週10枚馬券を購入するペース
mapMap = {}
for key_index, (key, datadict) in enumerate(dataMap.items()):
dftrain, dfvalid, dftest = datadict["train"], datadict["valid"], datadict["test"]
dftrlist, dfvlist, dftlist = [], [], []
dftrmap, dfvmap, dftmap = {}, {}, {}
for pred_fav in range(1, 19):
# region
dftrmap[f"fav{pred_fav}"] = {}
dfvmap[f"fav{pred_fav}"] = {}
dftmap[f"fav{pred_fav}"] = {}
dftrrow = {}
dfvrow = {}
dftrow = {}
idftrain = dftrain[
# dftrain["raceDate"].le(dftrain["raceDate"].max() - pd.Timedelta(180, unit="D")) &
# dftrain["raceDate"].ge(dftrain["raceDate"].max() - pd.Timedelta(365, unit="D")) &
dftrain["raceDate"].ge(dftrain["raceDate"].max() - pd.Timedelta(backDays, unit="D")) &
dftrain["pred_rank"].isin([1]) &
dftrain["raceGrade"].ge(raceGrade) &
dftrain["raceGrade"].lt(cutRaceGrade) &
dftrain["pred_odds_rank"].le(pred_fav) &
dftrain["pred_odds_rank"].gt(cutFav)
]
idfvalid = dfvalid[
dfvalid["pred_rank"].isin([1]) &
dfvalid["raceGrade"].ge(raceGrade) &
dfvalid["raceGrade"].lt(cutRaceGrade) &
dfvalid["pred_odds_rank"].le(pred_fav) &
dfvalid["pred_odds_rank"].gt(cutFav)
]
idftest = dftest[
dftest["pred_rank"].isin([1]) &
dftest["raceGrade"].ge(raceGrade) &
dftest["raceGrade"].lt(cutRaceGrade) &
dftest["pred_odds_rank"].le(pred_fav) &
dftest["pred_odds_rank"].gt(cutFav)
]
# endregion
for qleft in np.arange(0, 1.0, 0.05):
target_column = "pred_odds"
# target_column = "pred_proba"
qbottom, qtop = idftrain[target_column].quantile(
[qleft, max(threash, qleft)])
idfv = idftrain[
idftrain[target_column].ge(qbottom) &
idftrain[target_column].le(qtop)
]
if (backDays/180)*betNum > len(idfv):
dftrrow[f"fav{pred_fav}-q{100*qleft:.0f}"] = {
"profit": round(idfv[idfv["label"].isin([1])]["odds"].sum(), 1),
"hitNum": idfv["label"].isin([1]).sum(),
"betNum": len(idfv),
"rRate": round(idfv[idfv["label"].isin([1])]["odds"].sum()/len(idfv), 2),
"hitRate": round(idfv["label"].isin([1]).mean(), 4)
}
dftrmap[f"fav{pred_fav}"]["q" + f"{100*qleft:.0f}".zfill(3)] = round(
idfv[idfv["label"].isin([1])]["odds"].sum()/len(idfv), 2)
else:
dftrmap[f"fav{pred_fav}"]["q" +
f"{100*qleft:.0f}".zfill(3)] = np.nan
idfv = idfvalid[
idfvalid[target_column].ge(qbottom) &
idfvalid[target_column].le(qtop)
]
if betNum > len(idfv):
dfvrow[f"fav{pred_fav}-q{100*qleft:.0f}"] = {
"profit": round(idfv[idfv["label"].isin([1])]["odds"].sum(), 1),
"hitNum": idfv["label"].isin([1]).sum(),
"betNum": len(idfv),
"rRate": round(idfv[idfv["label"].isin([1])]["odds"].sum()/len(idfv), 2),
"hitRate": round(idfv["label"].isin([1]).mean(), 4)
}
dfvmap[f"fav{pred_fav}"]["q" + f"{100*qleft:.0f}".zfill(3)] = round(
idfv[idfv["label"].isin([1])]["odds"].sum()/len(idfv), 2)
else:
dfvmap[f"fav{pred_fav}"]["q" +
f"{100*qleft:.0f}".zfill(3)] = np.nan
idfv = idftest[
idftest[target_column].ge(qbottom) &
idftest[target_column].le(qtop)
]
if betNum > len(idfv):
dftrow[f"fav{pred_fav}-q{100*qleft:.0f}".zfill(3)] = {
"profit": round(idfv[idfv["label"].isin([1])]["odds"].sum(), 1),
"hitNum": idfv["label"].isin([1]).sum(),
"betNum": len(idfv),
"rRate": round(idfv[idfv["label"].isin([1])]["odds"].sum()/len(idfv), 2),
"hitRate": round(idfv["label"].isin([1]).mean(), 4)
}
dftmap[f"fav{pred_fav}"]["q" + f"{100*qleft:.0f}".zfill(3)] = round(
idfv[idfv["label"].isin([1])]["odds"].sum()/len(idfv), 2)
else:
dftmap[f"fav{pred_fav}"]["q" +
f"{100*qleft:.0f}".zfill(3)] = np.nan
dftrlist += [pd.DataFrame.from_dict(dftrrow, orient="index")]
dfvlist += [pd.DataFrame.from_dict(dfvrow, orient="index")]
dftlist += [pd.DataFrame.from_dict(dftrow, orient="index")]
dftr = pd.DataFrame.from_dict(dftrmap)
dfv = pd.DataFrame.from_dict(dfvmap)
dft = pd.DataFrame.from_dict(dftmap)
mapMap[key] = {
"train": dftr,
"valid": dfv,
"test": dft
}
qmap = ["q" + f"{100*qleft:.0f}".zfill(3)
for qleft in np.arange(0, 1, 0.05)]
fig, axis = plt.subplots(1, 2)
fig.set_figwidth(20)
fig.set_figheight(5)
plt.suptitle(f"Index: {key_index}, {key}")
fav_columns = [f"fav{n}" for n in range(cutFav+1, 19)]
plt.title("学習データ")
sns.heatmap(100*dftr[fav_columns].loc[qmap], ax=axis[0], annot=True, center=100,
fmt=".0f", cmap="coolwarm", vmax=200, vmin=0)
plt.title("検証データ")
sns.heatmap(100*dfv[fav_columns].loc[qmap], ax=axis[1], annot=True, center=100,
fmt=".0f", cmap="coolwarm", vmax=200, vmin=0)
# sns.heatmap(100*dft[fav_columns].loc[qmap], ax=axis[2], annot=True, center=100,
# fmt=".0f", cmap="coolwarm", vmax=200, vmin=0)
plt.tight_layout()
plt.show()
最良モデルの選択条件¶
最良モデルの選択条件を以下とする
- 横軸が
fav18の分布で最も縦軸の分位が低いものをみる - 学習データで項番1で選択したマスの回収率が100%を超え かつ 検証データの同マスが最も高いもの
上記2つに当てはまるものを最良モデルとします。
よって、まずは項番1のマスの中で、学習データでの回収率が100%を超えているモデルは以下の13モデル
1, 2, 5, 6, 7, 9, 11, 12, 13, 15, 16, 18, 19
対象のモデルの検証データの回収率は以下
39%, 79%, 62%, 73%, 41%, 56%, 35%, 65%, 83%, 119%, 124%, 43%, 74%
よって条件に当てはまるモデルは、インデックス16番のモデルだと分かった。
また、上記のような選択条件にした理由としては、以下の2つです
- なるべく多くの人気を対象にすることで、本命派と穴馬派どちらにも対応できるAIが良い
本命も当てて穴馬も当てるAIは魅力的という理由 - なるべく低い分位にすることで、ある程度の馬券購入枚数を確保したい
よくある回収率140%超えました的な釣り記事では、蓋を開けると1年間で70枚しか馬券を買わないという現実的でない馬券購入枚数で高い回収率を出したと豪語しているものが多い
そのため、今回のように半年間で250枚馬券を購入するというベット枚数を決めて、それに該当する分位に絞り込みたかったのが理由
8.最良のモデルの成績確認¶
検証データとテストデータについて、pred_rankが1位のデータについて実際の着順の分布とその累積分布を確認してみます。
まずは、インデックス16番のモデルを取り出します。
best_index = 16
bestModel = list(dataMap.values())[best_index]
dftrain, dfvalid, dftest = bestModel["train"], bestModel["valid"], bestModel["test"]
# 最良モデル選択条件に当てはまる横軸の人気の値と分位を取り出す
pred_fav = 18
target_threash = int(list(mapMap.values())[
best_index]["test"]["fav18"].dropna().index[0][1:])/100
学習データ、検証データ、テストデータの順で着順の分布を確認する。
print("pred_rank=1に賭けたときの着順の分布")
display(
pd.concat(
[
dftrain[dftrain["pred_rank"].isin([1])]["label"].value_counts(
).sort_index().to_frame(name="train").T,
dftrain[dftrain["pred_rank"].isin([1])]["label"].value_counts().sort_index(
).to_frame(name="累積分布").T.cumsum(axis=1)/dftrain["pred_rank"].isin([1]).sum()*100
]
)
)
display(
pd.concat(
[
dfvalid[dfvalid["pred_rank"].isin([1])]["label"].value_counts(
).sort_index().to_frame(name="valid").T,
dfvalid[dfvalid["pred_rank"].isin([1])]["label"].value_counts().sort_index(
).to_frame(name="累積分布").T.cumsum(axis=1)/dfvalid["pred_rank"].isin([1]).sum()*100
]
)
)
display(
pd.concat(
[
dftest[dftest["pred_rank"].isin([1])]["label"].value_counts(
).sort_index().to_frame(name="test").T,
dftest[dftest["pred_rank"].isin([1])]["label"].value_counts().sort_index(
).to_frame(name="累積分布").T.cumsum(axis=1)/dftest["pred_rank"].isin([1]).sum()*100
]
)
)
学習データでさえ1着の的中率は9%弱と大して高くはなく、テストデータでも8%弱と学習データとおおよそ差はないので、それなりに汎化性能は保てているようである。
続いて、実際に賭けた馬の実際の人気がどうだったかを見てみる
print("pred_rank=1に賭けたときの人気の分布")
display(
pd.concat(
[
dftrain[dftrain["pred_rank"].isin([1])]["favorite"].value_counts(
).sort_index().to_frame(name="train").T,
100*dftrain[dftrain["pred_rank"].isin([1])]["favorite"].value_counts().sort_index(
).to_frame(name="累積分布").T.cumsum(axis=1)/dftrain["pred_rank"].isin([1]).sum()
]
)
)
display(
pd.concat(
[
dfvalid[dfvalid["pred_rank"].isin([1])]["favorite"].value_counts(
).sort_index().to_frame(name="valid").T,
100*dfvalid[dfvalid["pred_rank"].isin([1])]["favorite"].value_counts().sort_index(
).to_frame(name="累積分布").T.cumsum(axis=1)/dfvalid["pred_rank"].isin([1]).sum()
]
)
)
display(
pd.concat(
[
dftest[dftest["pred_rank"].isin([1])]["favorite"].value_counts(
).sort_index().to_frame(name="test").T,
100*dftest[dftest["pred_rank"].isin([1])]["favorite"].value_counts().sort_index(
).to_frame(name="累積分布").T.cumsum(axis=1)/dftest["pred_rank"].isin([1]).sum()
]
)
)
結果から、おおよそまんべんなくまばらの人気にベットすることが出来ているのが分かり、人気に依らない予想AIが出来ているのが分かる
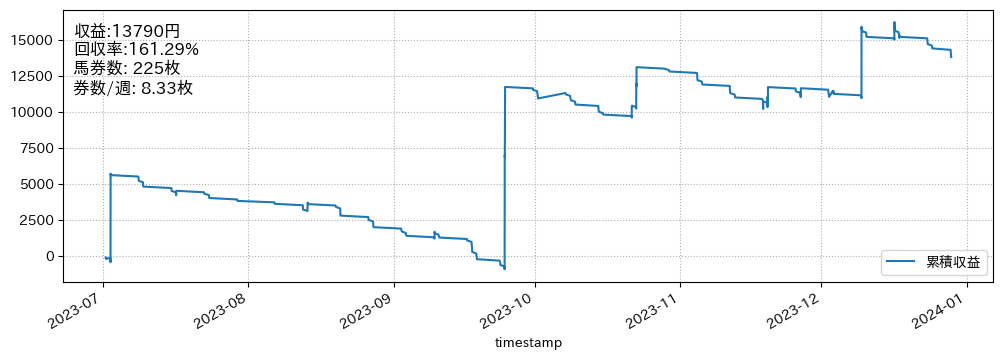
回収率の確認:半年間で回収率160%超を達成!!¶
# region フィルタ
idftrain = dftrain[
dftrain["raceDate"].ge(dftrain["raceDate"].max() - pd.Timedelta(backDays, unit="D")) &
dftrain["pred_rank"].isin([1]) &
dftrain["raceGrade"].ge(raceGrade) &
dftrain["raceGrade"].lt(cutRaceGrade) &
dftrain["pred_odds_rank"].le(pred_fav)
]
qbottom, qtop = idftrain[target_column].quantile(
[target_threash, max(threash, target_threash)])
dfa = dftest
# dfa = dfvalid
idfvalid = dfa[
dfa["pred_rank"].isin([1]) &
dfa["raceGrade"].ge(raceGrade) &
dfa["raceGrade"].lt(cutRaceGrade) &
dfa["pred_odds_rank"].le(pred_fav)
]
idfv2 = idfvalid[
idfvalid["pred_odds"].ge(qbottom) &
idfvalid["pred_odds"].le(qtop)
] # .iloc[:betNum]
# endregion
idfv2["収益"] = idfv2["odds"] * idfv2["label"].isin([1]) - 1
idfv2["week"] = idfv2["raceDate"].dt.isocalendar()["week"]
idfv2["timestamp"] = (idfv2["raceDate"].dt.strftime(
"%Y-%m-%d ") + idfv2["startTime"]).astype("datetime64[ns]")
plt.figure(figsize=(12, 4))
(idfv2.set_index("timestamp").sort_index()
["収益"].cumsum()*100).plot(label="累積収益")
y = idfv2["収益"].sum()
plt.text(
0.01, .95,
f"収益:{y*100:.0f}円\n回収率:{100+y*100/len(idfv2):.2f}%\n馬券数: {len(idfv2)}枚\n券数/週: {len(idfv2)/idfv2['week'].nunique():.2f}枚",
transform=plt.gca().transAxes, # 軸に相対的な座標系を指定
fontsize=12,
verticalalignment='top', # 上寄せ
horizontalalignment='left'
)
plt.legend(loc="lower right")
plt.grid(ls=":")
plt.show()
結果を見ると、半年間で馬券購入枚数が225枚でおおよそ毎週8枚馬券を購入して、収益13,790円で驚異の回収率161%を達成しているのが分かります。
9.最後に¶
今回の結果から言えることは、深層学習を使った競馬予想AIでもかなり優秀な成績を出せる可能性があることが分かった。
ただし、今回の結果から注意してもらいたいのは、あくまでこれはルールベースによる買い目の最適化をしているだけにすぎず、当然ながら別の期間で試すとボロボロの成績になる可能性が十分にある。
そのため、将来的には、買い目も最適化するようなアーキテクチャを開発する必要があるため、まだまだ課題は山盛りである。
今回の結果を良いものとするか、悪いものとするかは読者の基準にゆだねることとします。
また、今回のモデルのパラメータは何かしらの形で共有できないか考え中です。
同じような分析をしたい方は、以下からソースを入手してください。
ゼロから作る競馬予想モデル・機械学習入門



コメント