【チュートリアル #3】深層学習を使った競馬予想AI作成¶
0-1.本講座の目的¶
深層学習を使った競馬予想AIの作成方法を本講座で解説していきます。
本講座を通して、PyTorchを使った競馬予想AIの深層学習モデルを自力で作れるようになることを目的としています。
まずは、深層学習の基本をおさえるため、
本Notebookでは、PyTorchを使った深層学習モデル作成のチュートリアルです。
本チュートリアルで扱う項目は以下
- 深層学習の基本的な知識
- 深層学習の学習過程
- データセット作成
- PyTorchのモデル構築方法:今回の内容
- 学習・推論の実行:今回の内容
- モデルの解釈方法:今回の内容
- モデル保存:今回の内容
前回の内容はこちら

0-2.前提環境¶
使用する深層学習ライブラリの紹介です。
- Python 3.10.5
- PyTorch 2.3.1
- GPU使う場合は:CUDA 18
ない場合はpip等でインストールしてください。
0-3.宣伝(環境準備)¶
本講座で扱うソースでは一部秘匿させていただいております。
ソースは「ゼロから作る競馬予想モデル・機械学習入門」にあるものを使用しています。
また、本Notebookは「dev-um-ai > notebook > DeepLearning > 0000-3_deeplearning_tutrial3.ipynb」にあります。
環境構築(パッケージ管理)はpoetryを使用しているので、プロジェクトファイルさえあればコマンド一発で環境構築が完了するので、ぜひご活用ください。
Bookersアカウントとご自身のYouTubeアカウントを連携していただき、以下のチャンネルを登録して頂きますと1000円引きで入手出来ますのでぜひ登録よろしくお願いいたします。
1.PyTorchのモデル構築方法¶
まずは前回作成したデータセットを読み込みます。
from torch.utils.data import Dataset # type: ignore
import torch # type: ignore
import pandas as pd # type: ignore
import pathlib
import pickle
import warnings
import sys
sys.path.append(".")
sys.path.append("../..")
from src.data_manager.dataset_tools import DatasetDict # noqa
# Datasetクラスを継承してカスタムDatasetクラスを作成
class CustomKaibaAIDataset(Dataset):
def __init__(self, dfnum: pd.DataFrame, dfcat: pd.DataFrame, dflabel: pd.Series) -> None:
self.numerous = dfnum
self.cat = dfcat
self.label = dflabel
def __len__(self):
return len(self.label)
def __getitem__(self, index):
num_fea = torch.tensor(self.numerous.loc[index], dtype=torch.float32)
# カテゴリ特徴量は一つ一つベクトル埋め込み層に突っ込むので、特徴量ごとに分けてtensor化しておく
cat_feas = torch.tensor(
[self.cat[c].loc[index] for c in self.cat.columns], dtype=torch.float32)
label = torch.tensor(self.label[index], dtype=torch.float32)
return num_fea, cat_feas, label
cache_dir = pathlib.Path("./data")
with open(cache_dir / "dataset_mapping.pkl", "rb") as f:
dataset_mapping: dict[str, DatasetDict] = pickle.load(f)
# モデル作成で使用する特徴量
# 量的変数の特徴量
num_feas = [
'distance_dev',
'number_dev',
'boxNum_dev',
'odds_dev',
'favorite_dev',
'age_dev',
'jweight_dev',
'weight_dev',
'gl_dev',
'race_span_fill_dev',
] + ['winR_stallion', 'winR_breed', 'winR_bStallion', 'winR_b2Stallion']
# 質的変数の特徴量
cat_feas = [
'place_en',
'field_en',
'sex_en',
'condition_en',
'jockeyId_en',
'teacherId_en',
'dist_cat_en',
'horseId_en',
"raceGrade", "stallionId_en", "breedId_en", "bStallionId_en", "b2StallionId_en"
]
PyTorchを使った深層学習モデルの作り方に入ります。
かなり簡単です。日本語の解説記事の沢山出ているので、この記事で理解が進まなかった方々は他のソースも確認してみると良いでしょう。
PyTorchのモデル構築で重要なことは以下です。
- torch.nn.Moduleクラスを継承し、initメソッドでネットワーク層を定義
- forwardメソッドに入力データの流れ(順伝播)を定義
以下は実装例です。
全特徴量を単純な全結合のニューラルネットワークで順伝播させるモデルを作ります。
また、カテゴリ特徴量は事前にベクトル埋め込みをしておきます。
import torch.nn as nn # type: ignore
import torch # type: ignore
import math
class KeibaAISecondModel(nn.Module):
def __init__(self, cat_num_list: list[int], numerous_feature_num: int) -> None:
super(KeibaAISecondModel, self).__init__()
cat_embed_list = []
self.embed_num_list = []
for cat_num in cat_num_list:
embed_num = round(math.sqrt(cat_num))
self.embed_num_list += [embed_num]
embed_layer = nn.Embedding(
cat_num, embed_num, padding_idx=cat_num-1)
cat_embed_list += [embed_layer]
# カテゴリのベクトル埋め込み用レイヤー
self.cat_embed_list = nn.ModuleList(cat_embed_list)
self.cat_num_list = cat_num_list
# 適当に2層ぐらいのNNを作る。
# 1つ目は入力層 → 隠れ層
self.linear_hidden_layer = nn.Linear(
numerous_feature_num+sum(self.embed_num_list),
1024
# 128
)
# 2つ目は隠れ層 → 隠れ層
self.linear_hidden_layer2 = nn.Linear(1024, 256)
# 3つ目は隠れ層 → 隠れ層
self.linear_hidden_layer3 = nn.Linear(256, 128)
# 4つ目は隠れ層 → 出力層
self.linear_hidden_layer4 = nn.Linear(128, 1)
# 最後に出力層 → sigmoid変換
self.sigmoid = nn.Sigmoid()
self.relu = nn.ReLU()
self.dropout = nn.Dropout(p=0.5)
def forward(self, x_num, x_cat_list):
x_cat_list = x_cat_list.int()
cat_embed_list = [self.cat_embed_list[idx](
x_cat) for idx, x_cat in enumerate(x_cat_list.T)]
cat_embed_list = torch.cat(
cat_embed_list, dim=1 if len(x_cat_list.shape) > 1 else 0)
x = torch.cat([x_num, cat_embed_list],
dim=1 if len(x_num.shape) > 1 else 0)
x = self.linear_hidden_layer(x)
x = self.relu(x)
x = self.dropout(x)
x = self.linear_hidden_layer2(x)
x = self.relu(x)
x = self.dropout(x)
x = self.linear_hidden_layer3(x)
x = self.relu(x)
x = self.dropout(x)
x = self.linear_hidden_layer4(x)
x = self.sigmoid(x)
return x
どういうモデルになっているのか可視化する
可視化にはtorchvizを使う方法が有名かと思いますので、そのサンプルを出しておきます。
また、解像度を高くするために「svg」形式で出すようにしてます。
大規模なモデルほど「png」形式にすると文字がつぶれて見れなくなるので、ぜひご参考にしてください。
from torchviz import make_dot # type: ignore
from torch.utils.data import DataLoader # type: ignore
dataset = dataset_mapping["2019first"]
dataset_loader = DataLoader(dataset.train_dataset, batch_size=1, shuffle=True)
for batch_data1, batch_data2, batch_label in dataset_loader:
break
model = KeibaAISecondModel(dataset.cat_num_list, len(num_feas))
model.eval()
y = model(batch_data1[0], batch_data2[0])
dot = make_dot(y, params=dict(model.named_parameters()))
# SVG形式でモデル構造の出力
dot.render('KeibaAISecondModel_Graph', format="svg")
かなり見づらいグラフが出てくるので、ここでは概念図をお見せします。
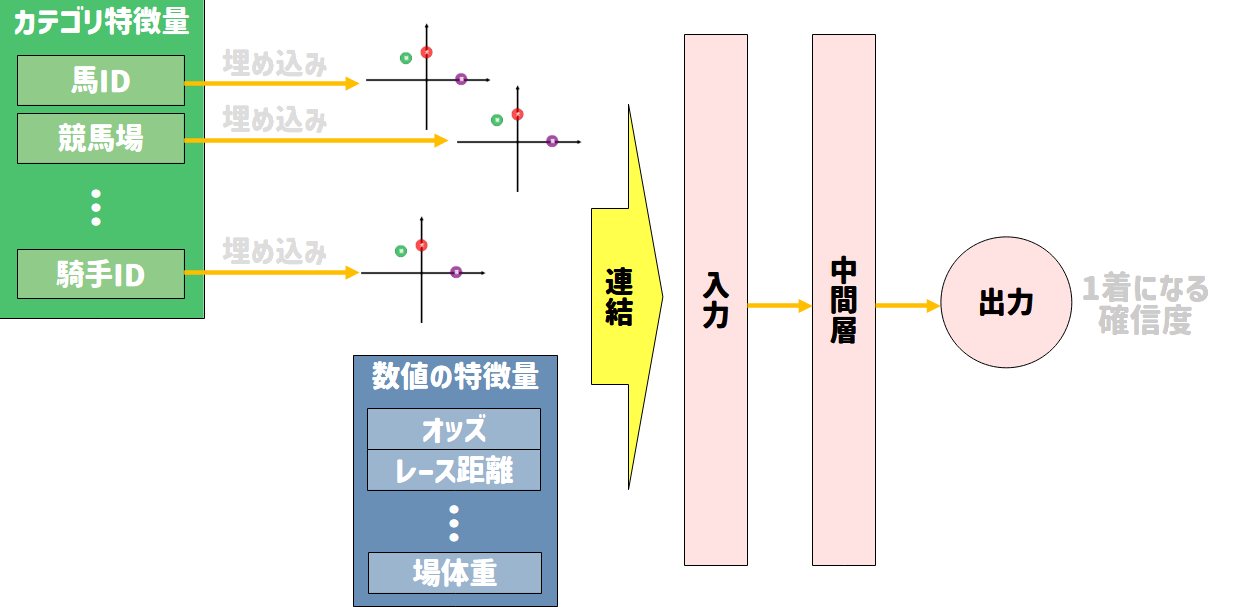
2.学習・推論の実行¶
2-1.損失関数¶
今回は1着になるか否かの2値分類の学習なので、バイナリ―クロスエントロピー誤差を使います。
有名な損失関数なので、PyTorch標準の損失関数が使えます。
- モデルの出力が確率値の場合:
torch.nn.BCELoss - モデルの出力が確率値でない場合:
torch.nn.BCEWithLogitsLoss
クロスエントロピー誤差とバイナリクロスエントロピー誤差の説明は以下を参照ください。

# 損失関数
loss_fn = nn.BCELoss()
2-2.オプティマイザ¶
オプティマイザというのは、モデルのパラメータの調整方法のことです。
正直ここをこだわるのはあまりお勧めしません。
基本的な種類を抑えて、タスクごとに使い分けるなどをする程度の理解で問題ありません。
タスクごとのおすすめのオプティマイザを以下に示します。
1. SGD (確率的勾配降下法)¶
torch.optim.SGDは最も基本的なオプティマイザで、勾配を単純に更新します。
学習率やモメンタム、または重み減衰(L2正則化)を調整できます。
- 適用例: 小規模なモデルや、特定の問題で安定した学習が求められる場合に使います。特に学習率スケジューラと組み合わせて使うことが一般的です。
- 特徴:
- シンプルで安定
- 非常に多くの計算リソースを消費しない
- 学習率のチューニングが重要
使用例:¶
optimizer = torch.optim.SGD(model.parameters(), lr=0.01, momentum=0.9)
2. Adam (適応的モーメンタム法)¶
torch.optim.Adamは、SGDを基にして、学習率を自動で調整し、パラメータごとに異なる学習率を持つことができます。
非常に広く使われており、収束速度が速いことが特徴です。
- 適用例: 大規模なネットワークや、パラメータのスケーリングが問題になる場合に便利です。特に深層学習モデルや経験的に学習がうまくいかない場合によく使われます。
- 特徴:
- 学習率を自動で調整
- 学習の初期段階で速く収束することが多い
- バッチサイズやデータセットの大きさに関わらず安定しやすい
使用例:¶
optimizer = torch.optim.Adam(model.parameters(), lr=0.001)
3. AdamW (Adam with Weight Decay)¶
torch.optim.AdamWは、AdamにL2正則化(重み減衰)を適用したバージョンです。
Adamのように学習率を調整しつつ、別にL2正則化を行いたい場合に使います。
- 適用例: L2正則化が必要な場合(例えば、過学習を防ぎたい場合)。特にトランスフォーマーモデルや深層学習において効果的です。
- 特徴:
- L2正則化を適切に処理
- Adamよりも性能が安定する場合がある
使用例:¶
optimizer = torch.optim.AdamW(model.parameters(), lr=0.001, weight_decay=0.01)
4. RMSprop (Root Mean Square Propagation)¶
torch.optim.RMSpropは、適応的学習率を使用し、勾配の二乗の平均で更新する手法です。
特にリカレントニューラルネットワーク(RNN)でよく使用されます。
- 適用例: RNNやLSTM、GRUなどのリカレントネットワークで使うことが多いです。学習が不安定な場合や、大きな勾配が問題になる場合にも使われます。
- 特徴:
- 勾配の変動が激しいときでも安定
- 非常に大きな勾配が発生する場合に有効
使用例:¶
optimizer = torch.optim.RMSprop(model.parameters(), lr=0.001, alpha=0.99)
5. Adagrad (適応型学習率法)¶
torch.optim.Adagradは、各パラメータに個別の学習率を割り当て、過去の勾配情報を基に学習率を調整します。
- 適用例: スパースなデータ(例えば、自然言語処理の単語埋め込みや稀な特徴)を扱う場合に有効です。学習率が徐々に減少するため、特定の条件下で非常に効果的です。
- 特徴:
- パラメータごとに異なる学習率を自動調整
- スパースデータに強い
使用例:¶
optimizer = torch.optim.Adagrad(model.parameters(), lr=0.01)
6. Adadelta¶
torch.optim.Adadeltaは、Adagradを改善したオプティマイザです。
学習率の減少を抑えるため、グラデーションに基づいて学習率を適応的に調整します。
- 適用例: Adagradと似たようなシチュエーションで使うことができますが、より適応的に学習率を調整するため、学習の安定性が向上します。
- 特徴:
- 長期的な学習において安定
- 学習率の急激な減少を防ぐ
使用例:¶
optimizer = torch.optim.Adadelta(model.parameters(), lr=1.0)
7. LBFGS (L-BFGS)¶
torch.optim.LBFGSは、BFGS法を基にした最適化手法です。
2次最適化法に近いもので、非常に高精度な最適化が行えますが、計算資源を大量に消費します。
- 適用例: 小さなデータセットで精度重視の学習を行いたい場合や、非常に高精度な解を求める場合に使います。深層学習ではあまり使われませんが、ある種の小規模な最適化問題には適しています。
- 特徴:
- 計算量が非常に大きい
- 高精度な解を求めるために適している
使用例:¶
optimizer = torch.optim.LBFGS(model.parameters(), lr=0.1)
まとめ¶
- SGD: 最もシンプルで、学習率のチューニングが重要。
- Adam/AdamW: 高速で安定した学習が可能。深層学習に最適。
- RMSprop: RNNなどで効果的。勾配の安定化が得意。
- Adagrad/Adadelta: スパースデータに適しており、学習率の調整が適応的。
- LBFGS: 高精度な最適化を要求する小規模な問題に使用。
学習するモデルやデータセットの特性に応じて、適切なオプティマイザを選ぶことが重要です。
一般的には、AdamやAdamWがほとんどの深層学習のタスクで広く使用されているオプティマイザです。
ということで、今回はAdamWを使ったオプティマイザにします。
# オプティマイザ
optimizer = torch.optim.AdamW(model.parameters(), lr=0.001, weight_decay=0.01)
2-3.学習の実行¶
モデル学習の基本的な流れは以下です。
- DatasetからDataLoaderの作成
- ミニバッチごとにモデルの推論 → 損失の計算 → パラメータの調整
- 項番2をDataLoaderで使用したDatasetの中身全てで実施
- 項番3を何回か繰り返す(エポック数のこと)
import tqdm # type: ignore
import numpy as np # type: ignore
# チュートリアルなので、dataset_mappingの内ひとつだけのdatasetを対象にモデルを学習してみる
target_dataset = dataset_mapping["2022second"]
# デバイスの設定(GPUが利用可能な場合)
device = torch.device('cuda:0' if torch.cuda.is_available() else 'cpu')
# device = "cpu"
# モデルの初期化
model = KeibaAISecondModel(
target_dataset.cat_num_list, len(num_feas)).to(device)
# 損失関数
loss_fn = nn.BCELoss()
# オプティマイザ
optimizer = torch.optim.AdamW(model.parameters(), lr=0.01, weight_decay=0.01)
# 1.DataLoaderの作成
train_dataloader = DataLoader(
target_dataset.train_dataset, batch_size=4096, shuffle=True)
valid_dataloader = DataLoader(target_dataset.valid_dataset, batch_size=len(
target_dataset.valid), shuffle=False)
test_dataloader = DataLoader(
target_dataset.test_dataset, batch_size=len(target_dataset.test), shuffle=False)
loss_list_all = []
# 学習ループ
num_epochs = 3
for epoch in range(num_epochs):
model.train() # 訓練モード
loss_list = []
with tqdm.tqdm(total=len(train_dataloader), desc=f"Train Epoch {epoch+1}/{num_epochs}. loss=None") as pbar:
for num_data, cat_data_list, labels in train_dataloader:
# データとラベルをGPUに転送
num_data, cat_data_list, labels = num_data.to(
device), cat_data_list.to(device), labels.to(device)
# 順伝播
optimizer.zero_grad() # 勾配を初期化
outputs = model(num_data, cat_data_list)
# 損失の計算
loss = loss_fn(outputs.squeeze(), labels)
# 逆伝播
loss.backward()
# 最適化
optimizer.step()
# ロスを記録
loss_list += [loss.item()]
pbar.update()
pbar.set_description(
desc=f"Train Epoch {epoch+1}/{num_epochs}. loss={np.mean(loss_list):.6f}")
loss_list_all += [loss_list]
model.eval() # 推論モード
# 検証データのロス確認
for num_data, cat_data_list, labels in valid_dataloader:
# データとラベルをGPUに転送
num_data, cat_data_list, labels = num_data.to(
device), cat_data_list.to(device), labels.to(device)
# 順伝播
outputs = model(num_data, cat_data_list)
# 損失の計算
loss = loss_fn(outputs.squeeze(), labels)
# テストデータのロス確認
for num_data, cat_data_list, labels in test_dataloader:
# データとラベルをGPUに転送
num_data, cat_data_list, labels = num_data.to(
device), cat_data_list.to(device), labels.to(device)
# 順伝播
outputs_test = model(num_data, cat_data_list)
# 損失の計算
loss_test = loss_fn(outputs_test.squeeze(), labels)
print(f"valid: {loss.item():.6f}, test: {loss_test.item():.6f}")
early stopを実装してないので、検証データのロスがEpoch 2以降から悪化してますが、学習データに関してはロスが減っているように見える。
※seed固定してないので環境ごとに結果が変わるかもしれません
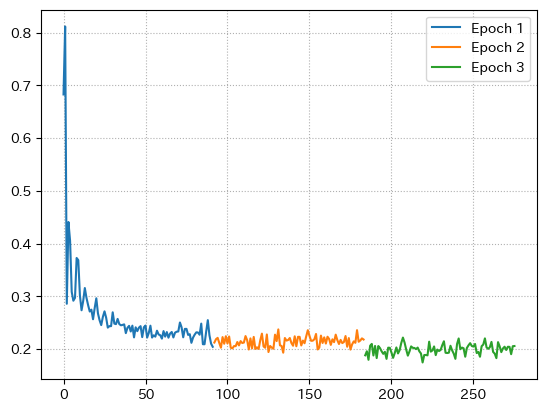
というわけで、ロスが学習するごとに減っているか確認してみましょう。
import matplotlib.pyplot as plt # type: ignore
import japanize_matplotlib # type: ignore
for idx, loss_list in enumerate(loss_list_all):
y = np.array(loss_list).reshape(-1)
x = list(range(len(y)*idx, len(y)*(idx+1)))
plt.plot(x, y, label=f"Epoch {idx+1}")
plt.grid(ls=":")
plt.legend()
plt.show()
epochごとにロスが減っているのが分かりますね。
2-4.推論の実行と結果の確認
検証データとテストデータそれぞれでどんな感じで予測されているのか確認してみましょう
予測確度をpred_probaカラムに、確度のランキングをpred_rankとしています。
dfvalid = target_dataset.valid.copy()
dfvalid["pred_proba"] = outputs.squeeze().to("cpu").detach().numpy()
dfvalid["pred_rank"] = dfvalid.groupby(
"raceId")["pred_proba"].rank(ascending=False).astype(int)
dftest = target_dataset.test.copy()
dftest["pred_proba"] = outputs_test.squeeze().to("cpu").detach().numpy()
dftest["pred_rank"] = dftest.groupby(
"raceId")["pred_proba"].rank(ascending=False).astype(int)
検証データとテストデータについて、pred_rankが1位のデータについて実際の着順の分布とその累積分布を確認してみます。
print("pred_rank=1に賭けたときの着順の分布")
display(
pd.concat(
[
dfvalid[dfvalid["pred_rank"].isin([1])]["label"].value_counts(
).sort_index().to_frame(name="valid").T,
dfvalid[dfvalid["pred_rank"].isin([1])]["label"].value_counts().sort_index(
).to_frame(name="累積分布").T.cumsum(axis=1)/dfvalid["pred_rank"].isin([1]).sum()
]
)
)
display(
pd.concat(
[
dftest[dftest["pred_rank"].isin([1])]["label"].value_counts(
).sort_index().to_frame(name="test").T,
dftest[dftest["pred_rank"].isin([1])]["label"].value_counts().sort_index(
).to_frame(name="累積分布").T.cumsum(axis=1)/dftest["pred_rank"].isin([1]).sum()
]
)
)
結果から実際に1着を一番多く当てることができているので、何かしらの特徴量を学習できていると考えられる。
ということで、ネタは割れているので人気別のベット回数も確認してみましょう。
print("pred_rank=1に賭けたときの人気の分布")
display(
pd.concat(
[
dfvalid[dfvalid["pred_rank"].isin([1])]["favorite"].value_counts(
).sort_index().to_frame(name="valid").T,
dfvalid[dfvalid["pred_rank"].isin([1])]["favorite"].value_counts().sort_index(
).to_frame(name="累積分布").T.cumsum(axis=1)/dfvalid["pred_rank"].isin([1]).sum()
]
)
)
display(
pd.concat(
[
dftest[dftest["pred_rank"].isin([1])]["favorite"].value_counts(
).sort_index().to_frame(name="test").T,
dftest[dftest["pred_rank"].isin([1])]["favorite"].value_counts().sort_index(
).to_frame(name="累積分布").T.cumsum(axis=1)/dftest["pred_rank"].isin([1]).sum()
]
)
)
結果から1番人気に一番賭けていることが分かり、1番人気から3番人気に全体の7割~8割を賭けていることから、オッズや人気の特徴量を目安にベットしていることが分かる。
これは、セカンドモデルでもどうようの特徴が出ているので、学習がうまくいっていると分かる。
収益、ベット回数、回収率を確認してみましょう
idfv = dfvalid[dfvalid["pred_rank"].isin([1]) & dfvalid["raceGrade"].ge(0)]
print(round(idfv[idfv["label"].isin([1])]["odds"].sum(), 1), len(
idfv), round(idfv[idfv["label"].isin([1])]["odds"].sum(), 1)/len(idfv))
idfv = dftest[dftest["pred_rank"].isin([1]) & dftest["raceGrade"].ge(0)]
print(round(idfv[idfv["label"].isin([1])]["odds"].sum(), 1), len(
idfv), round(idfv[idfv["label"].isin([1])]["odds"].sum(), 1)/len(idfv))
結果から回収率が7割,8割程度なので1番人気に賭け続けた場合と大差ない回収率であることが分かる。
3.モデルの解釈
ここでは、学習した深層学習モデルを評価する、言わば、LightGBMでいうところの特徴量重要度に近しい、SHAP値というものを使ってモデルを解釈する手法をご紹介します。
SHAP値とは?¶
SHAP値(Shapley Additive Explanations)は、機械学習モデルの予測に対する各特徴量の貢献度を測る指標です。
ゲーム理論に基づき、各特徴量が予測値にどれだけ影響を与えたかを定量的に評価します。
SHAP値は、特徴量が予測に与える影響を個別に、かつ公平に分配する方法を提供し、モデルの解釈性を高めるものになります。
より詳しい解説をみたい方は以下の記事をご覧ください。

SHAPのインストール¶
それでは、先ほど作成した深層学習モデルを解釈してみましょう。
「ゼロから作る競馬予想モデル・機械学習入門」のソースをお使いの方は、モデル解釈用のライブラリ「shap」を以下のようにして追加してください。
※この際必ず「poetry.lock」ファイルがあるフォルダがカレントディレクトリになっていることを確認してください
poetry lock –no-update
poetry add shap
pipでバージョン管理している方は以下を実行
pip install shap
SHAP値の算出¶
コード自体はその辺に落ちているサンプルコードを一部拝借しています。
PyTorchやKeras(tensorflow)などの場合は、DeepExplainerを使うと良いとあるのですが、なぜかbackwaordがうまくいかなかったので別の方法としてKernelExplainerを使います。
SHAP値の出し方は、最初にExplainerのインスタンス作成する際に、SHAP値の評価用に背景データを渡してあげる必要があります。
この背景データはモデルの平均的な振る舞いの基準として扱われ、個別のデータポイントの特徴がどのようにモデルの予測に影響を与えるかを評価しています。
original_num_feas = [col.split("_dev")[0] for col in num_feas]
original_cat_feas = [col.split(
"Id_en")[0] + "Name" if "Id_en" in col and ("jockey" not in col and "teacher" not in col) else col.split("_en")[0] for col in cat_feas]
import shap # type: ignore
shap.initjs()
# backgroud dataの指定:ここは学習データから。100件超えてくると処理が遅くなるので注意
x_inputs = target_dataset.train.sample(150, random_state=777)[
num_feas+cat_feas]
model.to("cpu")
model.eval()
def func(dfvalid):
# model.to(device)
with torch.no_grad():
x1 = torch.tensor(dfvalid[:, :len(num_feas)]).float()
x2 = torch.tensor(dfvalid[:, len(num_feas):]).int()
# x1.to(device)
# x2.to(device)
output = model(x1, x2).numpy().reshape(-1)
return output
explainer = shap.KernelExplainer(
func, x_inputs.values)
# 分析対象のデータ。ここで選択したデータのSHAP値を計算する。特徴量等が多い場合も恐らく処理に時間がかかります
x_test = target_dataset.valid.iloc[1:].sample(99, random_state=777)
x_test = pd.concat([target_dataset.valid.iloc[[0]], x_test])[num_feas+cat_feas]
shap_values = explainer.shap_values(x_test)
shap_valuesの変数には、SHAP値算出のために指定したx_testの各データの特徴量ごとのSHAP値が入っています。
実際にデータの形式も同じになってます。
shap_values.shape, x_test.shape
つまり、shap_valuesの一つ目のインデックスは、x_testの一つ目のデータに対応しています。
次で紹介するSHAP値のプロットで、これらの対応があることに注意してサンプルコードをご覧ください。
各特徴量の寄与度の確認¶
summary_plot:特徴量の全体的な寄与を確認¶
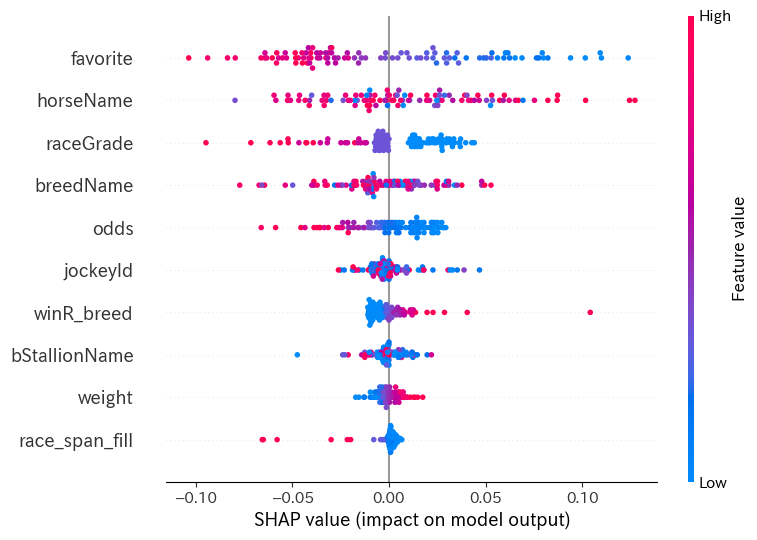
縦軸に各特徴量、横軸に寄与度を表しています。
グラフ上の点は各データを表しており、赤色であればあるほどデータに対するその特徴量の寄与が大きいことを表すそうです。
(ちょっと理解が甘いので調べてもらう方が良いです。)
x_test_org = target_dataset.valid.loc[x_test.index][original_num_feas +
original_cat_feas].copy()
shap.summary_plot(
shap_values,
x_test,
feature_names=original_num_feas+original_cat_feas,
max_display=10 # 表示されるグラフの大きさを調整します。あまりにも寄与が小さいものは非表示にされます。
)
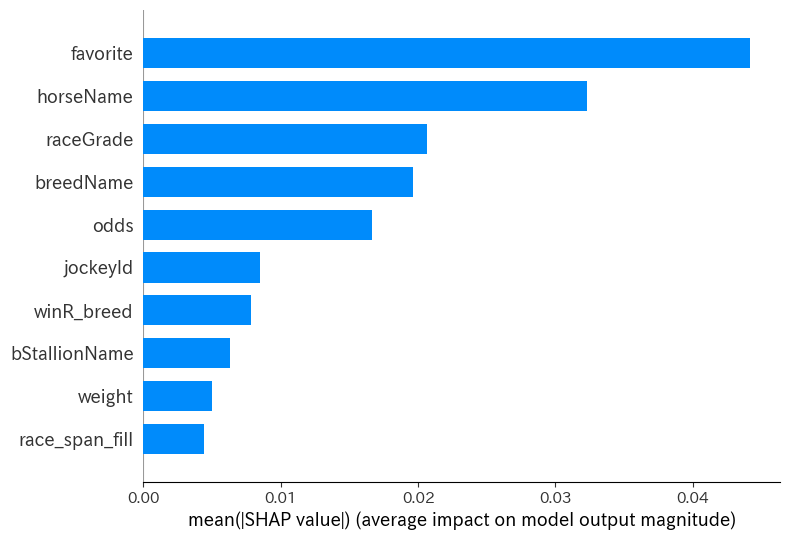
このsummary_plotは特徴量重要度的な形で出すことができます。
実態としては、全データに対するSHAP値の絶対値の平均を出してくれてます。
shap.summary_plot(
shap_values,
x_test,
feature_names=original_num_feas+original_cat_feas,
plot_type="bar",
max_display=10
)
force_plot:予測データに対する各特徴量の寄与度の詳細¶
ちなみに、この寄与度であるSHAP値というのは、以下の関係があります。
(データAに対するモデルの予測値) = (背景データのSHAP値の期待値) + (データAに対する全特徴量のSHAP値の和)
# たとえば、インデックス0のデータに対するモデルの予測値 pred_proba は以下
print("モデルの予測値: \t\t\t", dfvalid.loc[x_test.iloc[0].name]["pred_proba"])
# 続いて、背景データのSHAP値の期待値 expected_value は以下
print("背景データのSHAP値の期待値: \t", explainer.expected_value)
# インデックス0のデータに対する全特徴量のSHAP値の和
print("全特徴量のSHAP値の和: \t\t", shap_values[0].sum())
# この3つの値は、以下の関係にある
print("\nモデルの予測値 = 背景データのSHAP値の期待値 + 全特徴量のSHAP値の和")
print("モデルの予測値: \t\t\t\t\t\t", dfvalid.loc[x_test.iloc[0].name]["pred_proba"])
print("背景データのSHAP値の期待値 + 全特徴量のSHAP値の和: \t",
explainer.expected_value + shap_values[0].sum())
上記のような関係を視覚的に分かりやすくしているのが、force_plotになります。
プロットの仕方には、データ単体で見る場合と複数で見る場合の2通りがあります。
単体で見る場合¶
以下のように一つだけのインデックスを指定して実行するだけです。
なんか横棒グラフみたいなのが出てきます。
このグラフの解釈は、赤色が背景データの期待値からプラスに予測値を押し上げることに貢献している特徴量で、青色が背景データの期待値からマイナスに予測値を押し下げることに貢献している特徴量になっています。
グラフ上に表示される「0.00」という値が、モデルの予測値担っています。
shap.force_plot(
explainer.expected_value,
shap_values[0],
x_test_org.iloc[0],
)
サイトを見てくださってる方々には、表示がされてないかと思いますので、イメージ画像を添付しておきます。

上記のような感じで、どの特徴量が予測値に対してどのくらい寄与しているかを幅で表現してくれます。
この図で言うと、favoriteの特徴量がモデルの予測に大きくマイナスの寄与をしていることと、raceGradeの特徴量がプラスに寄与しているといったことが分かります。
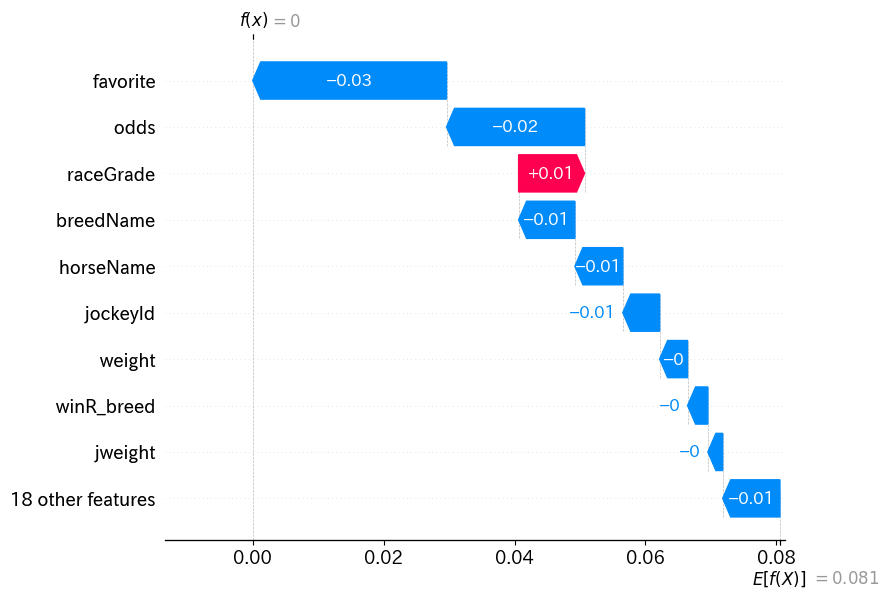
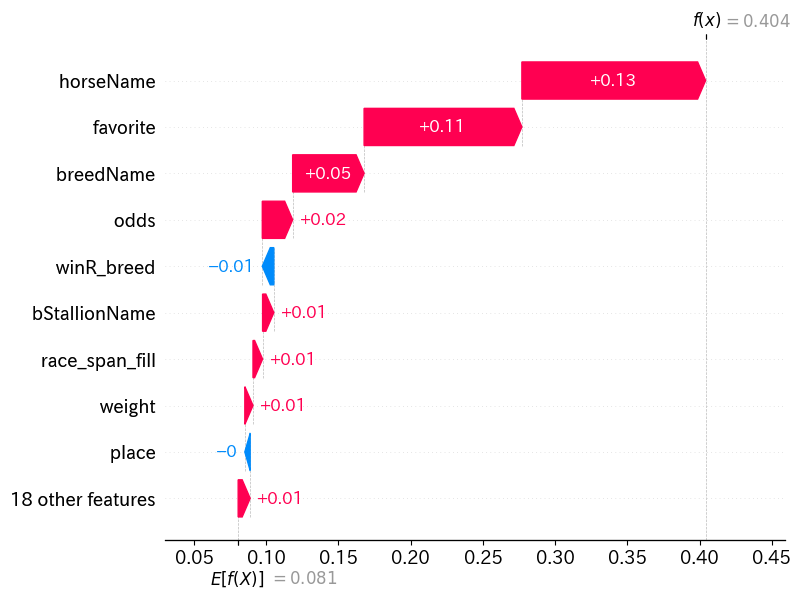
上記の横棒グラフではあまりイメージつかない場合は、以下のようにウォーターフォール形式でプロットすることもできます
shap.plots._waterfall.waterfall_legacy(
explainer.expected_value,
shap_values[0],
x_test_org.iloc[0],
)
ウォーターフォールで出すと、背景データの期待値から各特徴量がどのくらいモデルの予測値を上げたり下げたりしているのかがより分かりやすく見れるかと思います。
今回で言うと、人気であるfavoriteの影響が強く出ており、favoriteの値が15であることから、モデルの予測値が下に押し下げられているのが良く分かるかと思います。
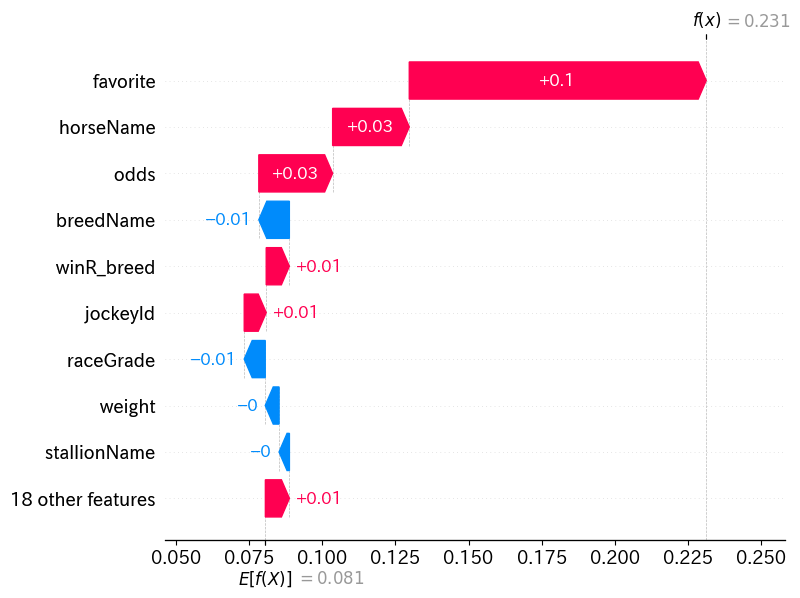
では、逆に1番人気のデータではどうなのかを見てみましょう。
fav1_index = x_test_org.reset_index(names="org_idx")[x_test_org.reset_index()[
"favorite"].isin([1])].sample(1).index.tolist()[0]
shap.plots._waterfall.waterfall_legacy(
explainer.expected_value,
shap_values[fav1_index],
x_test_org.iloc[fav1_index],
)
こちらは逆に、favoriteの特徴量によってモデルの予測値が大きく押し上げられているのが分かります。
それでは、1番人気の影響諸々あってSHAP値が最も高くなっているデータではどうなっているかも見てみましょう
max_index = shap_values.sum(axis=1).argmax()
shap.plots._waterfall.waterfall_legacy(
explainer.expected_value,
shap_values[max_index],
x_test_org.iloc[max_index],
)
なんとなく見てみましたが、こんな感じで色々な特徴量が予測値にプラスに働いていることが分かります。
こういうのが分かると、なぜこのデータはこんな予想ができたのか?といった際に、この特徴量が効いているからといった説明をすることが出来ます。
全体で見る場合¶
全体で見る場合は、インデックスの指定を無くして実行するだけです。
この場合、ウォーターフォールのグラフは出せないので、force_plotの結果のみお見せします。
shap.force_plot(
explainer.expected_value,
shap_values,
x_test_org,
)
【イメージ画像】
- データ点とモデルの予測値の関係
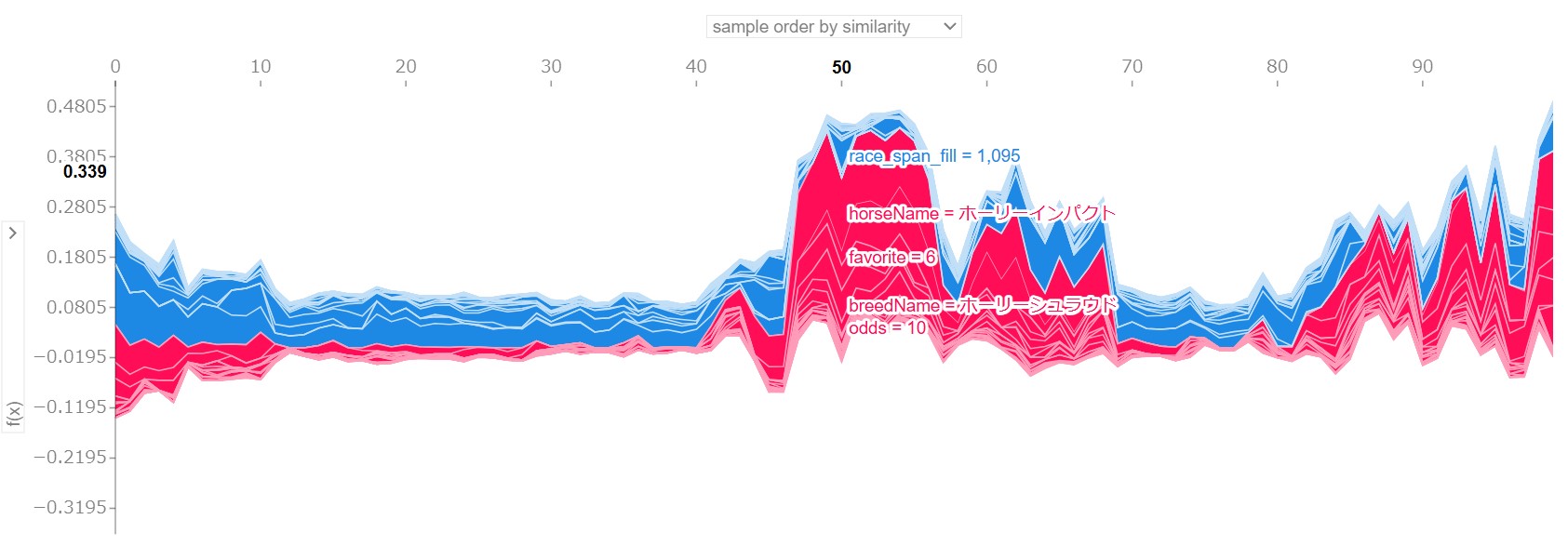
これだけ見せられても…って感じだと思いますが、この結果は色々と弄ることができて、縦軸にモデルの予測値があり、横軸が各データになります。
赤色と青色はこれまでご説明した通りです。
縦軸や横軸のラベルを変更することができまして、横軸に「favorite」を指定すると、favoriteが取り得る値が横軸に変わります。
この時の縦軸は、各favoriteの値に対するモデルの予測値の平均値になっています。
では逆に縦軸を、例えば「odds」とかに変更した場合、縦軸の値は横軸のfavoriteの値ごとのoddsの寄与度の平均値を表しています。
【イメージ画像】
- 人気別のオッズの寄与度
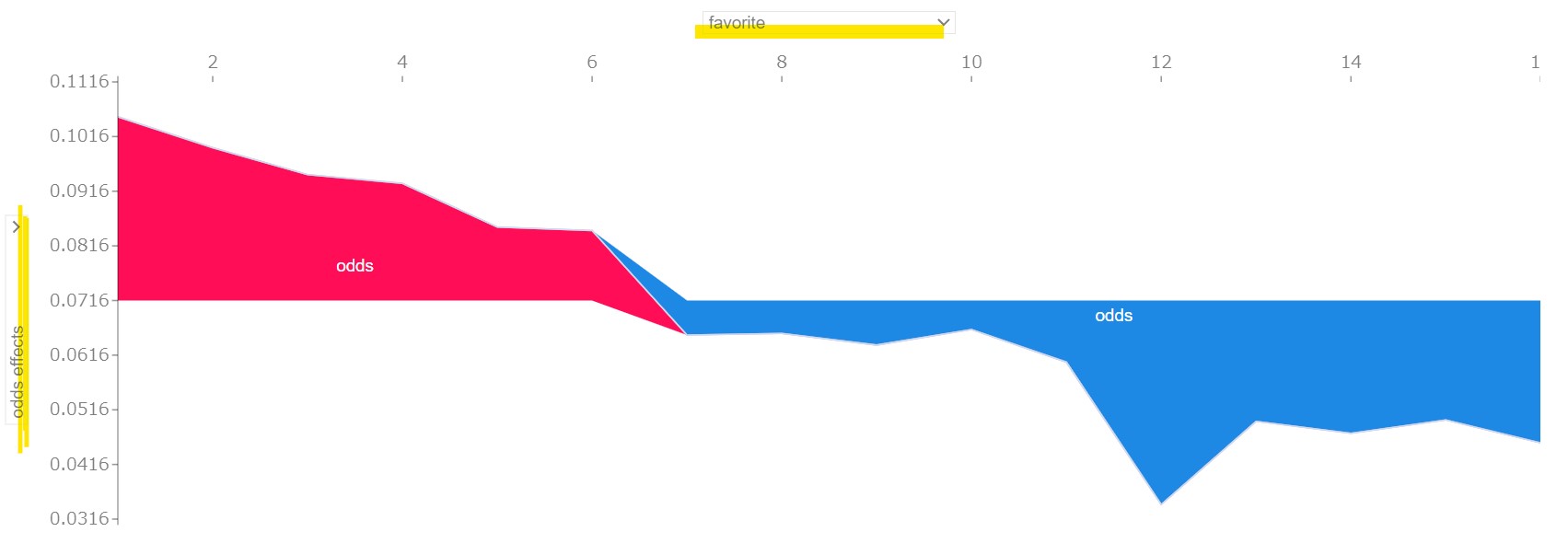
このグラフでみると、7番人気あたりからオッズの寄与度はプラスからマイナスに反転して評価されるようになることが分かります。
この辺のグラフは、実際に本Notebookのコードを実行すると色々と弄ることができます。
本Notebookのコードの一部は「ゼロから作る競馬予想モデル・機械学習入門」のソースを使用していますので、実行する際はその点配慮しながらリファクタリングしてください。
以上のようなやり方で、モデルのふるまいを確認することができるので、ぜひご活用ください。
4.モデルの保存¶
ここでは、せっかくモデル作ったのだから、いつでもロードして使えるように保存しておきたいって方向けの内容です。
モデルの保存方法はいくつかありますが、もっともサイズが軽いやり方でモデルの保存をしましょう。
モデルのパラメータ保存¶
model_dir = pathlib.Path("./model")
model_dir.mkdir(exist_ok=True)
# モデルのパラメータを保存
torch.save(model.state_dict(), model_dir / "tutrial_model_weights.pth")
上記のような感じで、モデルのパラメータを保存することができます。
保存したパラメータを読み込みたい場合は次の話になります。
モデルのパラメータの読み込み¶
モデルを読み込む際には、もともとモデルはGPU経由かCPU経由で保存されているのかに注意して読み込む必要があります。
1. GPUで保存したモデルをCPUで読み込む¶
GPUで保存したモデルをCPUで読み込む場合、torch.load関数にmap_location引数を使ってデバイスを指定します。これにより、モデルの重みがGPUからCPUに変換され、読み込み時のエラーを防げます。
# GPUで保存されたモデルをCPUで読み込む
model = YourModel()
checkpoint = torch.load(model_dir / "tutrial_model_weights.pth", map_location=torch.device("cpu"))
model.load_state_dict(checkpoint)
2. CPUで保存したモデルをGPUで読み込む¶
逆に、CPUで保存されたモデルをGPUで読み込む場合も同様にmap_locationでGPUを指定します。この時、モデルを読み込んだ後、モデルをGPUに移動させます。
# CPUで保存されたモデルをGPUで読み込む
model = YourModel()
checkpoint = torch.load(model_dir / "tutrial_model_weights.pth", map_location=torch.device("cuda"))
model.load_state_dict(checkpoint)
model.to("cuda") # モデル全体をGPUに移動
3. GPU間での読み込み¶
異なるGPUデバイス間で読み込む場合にもmap_locationが有効です。たとえば、GPU 0 で保存してGPU 1で読み込みたい場合には、次のように指定します。
# GPU 0で保存されたモデルをGPU 1で読み込む
checkpoint = torch.load(model_dir / "tutrial_model_weights.pth", map_location={"cuda:0": "cuda:1"})
model.load_state_dict(checkpoint)
model.to("cuda:1")
4. モデルとオプティマイザを両方読み込む場合¶
モデルとオプティマイザの両方の状態を読み込む際も同様にデバイスを指定します。
# GPUで保存されたチェックポイントをCPUで読み込む
checkpoint = torch.load(model_dir / "tutrial_model_weights.pth", map_location=torch.device("cpu"))
model.load_state_dict(checkpoint['model_state_dict'])
optimizer.load_state_dict(checkpoint['optimizer_state_dict'])
注意点¶
- 異なるデバイスでの保存・読み込み時は、必ず
map_locationを指定して正しいデバイスにマッピングしてください。 model.to("cuda")の後も、データをGPU上で処理する場合にはデータも.to("cuda")で移動させる必要があります。
5.まとめ¶
以上で、深層学習のチュートリアル終了になります。
ここまで御覧いただきありがとうございました。
「ゼロから作る競馬予想モデル・機械学習入門」では、今回のように競馬のデータ収集から分析、AIモデルの作成と結果の解釈と様々な手法をご紹介し、儲かる競馬AIの作成を目指しています。
BookersのアカウントとYouTubeのアカウントを連携して頂き、以下の私のチャンネルを登録して頂くと、「ゼロから作る競馬予想モデル・機械学習入門」を1,000円引きで購入できますので、ぜひよろしくお願いいたします。
それでは、次回はいよいよ本ソースに深層学習の機能を追加して、LightGBMで作成したサードモデルを深層学習で再現するモデル作成手順を公開いたします。
PyTorchによる醍醐味であるモデルの構築と損失関数のカスタマイズの柔軟性をご紹介できればと考えています。


コメント