7.過去成績の分析
セカンドモデルの作成では血統情報を考慮したモデルの開発を目的としていた。
これは競走馬が持つ血統が着順に影響を与えていることを前提としており、
いわばその競走馬の基礎力が血統に当たるものだと考えていた。
一方で今回の過去の成績から着順を予想しようとする考え方は、
その競走馬の実力を測ることに等しい。
これからの過去成績の分析から期待することは、
その競走馬の脚質を分析できること
レース展開の分析ができること
競馬場×馬場×距離カテゴリごとに、勝ちやすい脚質が分析できること
上記3点を知ることができないか取り組むこととする
今日やること
- 過去成績の調べ方
ソースの一部は有料のものを使ってます。
同じように分析したい方は、以下の記事から入手ください。
import pathlib
import warnings
import lightgbm as lgbm
import pandas as pd
import tqdm
import datetime
import matplotlib.pyplot as plt
import japanize_matplotlib
import seaborn as sns
import numpy as np
import sys
sys.path.append(".")
sys.path.append("..")
from src.data_manager.preprocess_tools import DataPreProcessor # noqa
from src.data_manager.data_loader import DataLoader # noqa
warnings.filterwarnings("ignore")
root_dir = pathlib.Path(".").absolute().parent
dbpath = root_dir / "data" / "keibadata.db"
start_year = 2000 # DBが持つ最古の年を指定
split_year = 2014 # 学習対象期間の開始年を指定
target_year = 2019 # テスト対象期間の開始年を指定
end_year = 2023 # テスト対象期間の終了年を指定 (当然DBに対象年のデータがあること)
# 各種インスタンスの作成
data_loader = DataLoader(
start_year,
end_year,
dbpath=dbpath # dbpathは各種環境に合わせてパスを指定してください。絶対パス推奨
)
dataPreP = DataPreProcessor()
df = data_loader.load_racedata()
dfblood = data_loader.load_horseblood()
df = dataPreP.exec_pipeline(
df, dfblood, ["s", "b", "bs", "bbs", "ss", "sss", "ssss", "bbbs"])
7-1.過去成績の調べ方
競走馬ごとに過去成績を見ることは、
- 脚質の確認
- 馬場適正や持ちタイムの確認
- レース展開の予想がしたい
簡単に上記のような理由があると考える
このうち、馬場適正については、定量的な評価軸が分からない
何を以って適性があると判断するのは個人の裁量に依ると考える
そのため、馬場適正については今回は考えないものとする
7-2.脚質の分析¶
脚質とは、競走馬がレースの序盤,中盤,終盤での
主な立ち位置をとるかを四種類に分けたもの
分類は以下
- 逃げ(にげ)
- 特徴: スタートから一気に前に出て、他の馬に追い越されないように先頭をキープする脚質。
特に短距離レースで有効。馬が他の馬に追いかけられると燃えるタイプの場合、この脚質が向いている。 - 戦術: スタートダッシュが非常に重要で、最初の数百メートルでリードを取る必要がある。
ペース配分を間違えると終盤にバテるリスクがある。
- 特徴: スタートから一気に前に出て、他の馬に追い越されないように先頭をキープする脚質。
- 先行(せんこう)
- 特徴: スタートから早めに中団から前方のポジションを取る脚質。
逃げ馬のすぐ後ろについて、直線で一気に抜き去る戦法を取ることが多い。ペースの読みが重要。 - 戦術: レース中盤までにポジションを確保し、後半に向けて徐々にペースを上げる。
無駄なエネルギーを使わずに、逃げ馬を追いかけることが求められる。
- 特徴: スタートから早めに中団から前方のポジションを取る脚質。
- 差し(さし)
- 特徴: 中団から後方の位置でレースを進め、終盤の直線で一気にスピードを上げて前の馬を抜き去る脚質。
ペースが速いレースや、前半で消耗した馬が多いときに有利。 - 戦術: 序盤はエネルギーを温存し、直線に入るところで仕掛ける。
直線が長いコースや、ペースが速いレースに向いている。
- 特徴: 中団から後方の位置でレースを進め、終盤の直線で一気にスピードを上げて前の馬を抜き去る脚質。
- 追い込み(おいこみ)
- 特徴: スタートでは最後方に位置し、最終コーナーから直線で一気に加速して前の馬をすべて抜き去る脚質。
特にペースが崩れたレースでの逆転劇が見どころ。 - 戦術: 最初はエネルギーを最大限に温存し、最後の直線に全てをかける。
追い込みはリスクが高く、ペースや展開に左右されやすい。
- 特徴: スタートでは最後方に位置し、最終コーナーから直線で一気に加速して前の馬をすべて抜き去る脚質。
名馬には差しの脚質が多いと言われているが、
これは差しという戦法を取るにはレース展開などの
周りの状況に合わせてタイミングよく前に飛び出せるという
器用な立ち回りが求められるため、
騎手の意図をよく理解できる利口さと
それを実行できる実力が必要となることから、
自然と能力の高い競走馬が差しの戦法を取るとされている
あと単純に差しで後方から最後の直線で一気に勝ちを奪うのは、
見ていて面白いしロマンがあるので、印象に残りやすいのもありそう
7-3.脚質はどうすれば求められるか¶
前提として、脚質とは戦法であることから最終コーナ通過時または上り3F到達時までの順位でどの立ち位置にいるかを示すものと考える
そのため、コーナ通過順位の1コーナと最終コーナをどの順位で通過したかでその競走馬の脚質が見えてくると考える
よってここではレースの最初のコーナ通過順位と最終コーナ通過順位の2つを使って脚質を調べる
7- 4.2021年までのデータに絞って脚質分析¶
また、今後のモデル分析に向けて未知データもある程度残しておきたい
よって、2021年までのデータを使って分析し、2022年のデータを未知データとする
idfb = df[(df["raceDate"].dt.year < 2022)]
idfb.shape
脚質とは、レースで馬郡のどの位置を走っているかなので、
コーナ通過順位にまつわるデータとして以下が該当していると考える
label_1C: 最初のコーナー通過時の順位label_lastC: 最終コーナー通過時の順位
また通過順位は出走頭数によってその数字の意味が違うので、出走頭数で通過順位を割って割合として扱うこととする
for col in ["label_1C", "label_lastC"]:
idfb[f"{col}_rate"] = (idfb[col].astype(
int)/idfb["horseNum"]).convert_dtypes()
idfb[["label_1C_rate", "label_lastC_rate"]]
7-5.脚質の分類¶
分類するための手法(クラスタリング)は有名なものとして、K-Means法がある。
このアルゴリズムは、データポイントを「k」個のクラスターに分けることを目的としている。
それぞれのクラスターは、平均(centroid)と呼ばれる中心点を持ち、その中心点からの距離が最も近いデータポイントをそのクラスターに割り当てる手法である。
つまり、今回の話で言えば、最初のコーナー通過順位と最終コーナー通過順位の2種類の特徴量を使ってK-Means法でクラスタリングすると、脚質を4つに分けられるだろうという魂胆である。
from sklearn.cluster import KMeans # KMeans法のモジュールをインポート
# クラスタ数
n_cls = 4
rate = 2.5
# クラスタリングする特徴量を選定
cluster_columns = ["label_1C_rate", "label_lastC_rate"]
cluster_columns2 = ["label_1C_rate", "label_lastC_rate2"]
kmeans = KMeans(n_clusters=n_cls) # 脚質が4種類なので、クラス数を4とする
idfb["label_lastC_rate2"] = rate*idfb["label_lastC_rate"]
kmeans.fit(idfb[cluster_columns2])
KMeans(n_clusters=4)
クラスタリングのラベルを追加
このとき、クラスタリングの中心点が毎度ランダムになっていて都合が悪い
なので、label_1C_rateの値が小さい順にクラスタを並び替える
idfb["cluster"] = kmeans.predict(idfb[cluster_columns2])
dfcluster = pd.DataFrame(
kmeans.cluster_centers_.tolist(), columns=cluster_columns
).sort_values(cluster_columns[0])
dfcluster["reCluster"] = list(range(n_cls))
idfb["cluster"] = idfb["cluster"].map(dfcluster["reCluster"].to_dict())
クラスタリングの中心点を確認
dfcluster
内容を見るに
reCluster: 0: 最初から最終コーナまで、前方の位置を取っているので「逃げ」の脚質に類似reCluster: 1: 最初から最終コーナまで、中央やや前方気味の位置なので「先行」の脚質に類似reCluster: 2: 最初から最終コーナまで、中央やや後方気味の位置なので「差し」の脚質に類似reCluster: 3: 最初から最終コーナまで、後方の位置を取っているので「追込」の脚質に類似
以上のようなクラスタリングが出来ている
よって、reClusterの値が小さい順に「逃げ」「先行」「差し」「追込」と名付ける
clsnames = ["逃げ", "先行", "差し", "追込"]
cls_map = {i: d for i, d in enumerate(clsnames)}
idfb["clsName"] = idfb["cluster"].map(cls_map)
idfb["clsName"]
7-6.脚質と特徴量の関係をみたい¶
簡単に散布図を使って2次元グラフ上でどういったデータがどういった脚質に分類されているのか確認する
# plt.figure(figsize=(12, 12))
plt.rcParams["font.size"] = 10
g = sns.scatterplot(idfb.drop_duplicates(cluster_columns).sort_values(
"clsName", key=lambda x: x.map({c: i for i, c in enumerate(clsnames)})),
x="label_1C_rate", y="label_lastC_rate", hue="clsName", alpha=0.5,)
plt.ylim(bottom=-0.0, top=1.05)
plt.grid(ls=":")
plt.scatter(dfcluster[cluster_columns[0]],
dfcluster[cluster_columns[1]]/rate, marker="X", s=100, c="black")
plt.legend(loc="best")
for txt, row in zip(clsnames, dfcluster[cluster_columns].values):
plt.text(row[0], row[1]/rate, s=txt, c="black",
weight="bold", size="xx-large")
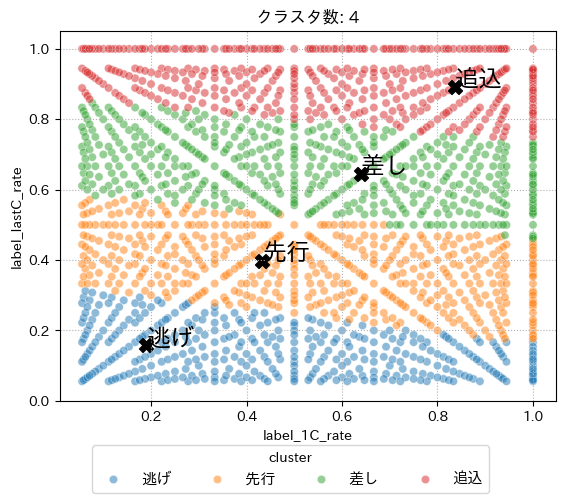
plt.title("クラスタ数: 4")
sns.move_legend(g, "upper left", bbox_to_anchor=(
0.05, -0.1), title='cluster', fontsize=11, ncol=4)
plt.show()
それなりにきれいな分かれ方をしている。
しかし、先行や差しのクラスタを見ると1Cを過ぎたところと最終コーナを通過した時を見るとかなり幅が広い。
つまり、1コーナを後方で通過したのち最終コーナを前方で通過すると先行の脚質に、逆に1Cを中間位置で通過後最終コーナを後方で通過すると差しの脚質になる。
クラスタ中心周辺のデータは皆が考える脚質の特徴に近い動きをするが、クラスタから遠い位置にいる点をどうすべきか困る瞬間がいつかくるかも。
そのため、クラスタ数を増やした場合も見てみようと思う
7-7.クラスタリングの深堀¶
もう少しクラスタリングのやり方を変える
以下の方針で分類
- 分類をさらに16クラスに増やす
- クラスタリング結果の中心点を
label_lastC_rateで昇順に並び変え - ソート結果の上から4つごとに
逃げ,先行,差し,追込に分類 - 分類した4グループ間で
label_1C_rateを昇順に並び変え
上記の方針の目的は、レースでは最終コーナ通過時に馬群のどの位置にいるかが重要だと考え、最もゴールに近いことからも早く通過すればするほど有利なのは間違いない
そのため、クラスタの中心点のlabel_lastC_rateの値が小さいデータほど逃げの戦法を取っている可能性が高いと考えた
そして、label_1C_rateが小さい場合は出走してから1コーナー通過した段階でレースのペースを作りリードする立場にあると見なせる
よってこのクラスタ分けの結果は、label_lastC_rateが小さいものから脚質の特徴を割り振り、脚質別にlabel_1C_rateが小さければ小さいほどペースメーカーを担うものを分類できると期待する
dflist = []
dfclist = []
sub_ncls = 4
# cluster_columns2 = cluster_columns
kmeans = KMeans(sub_ncls*n_cls)
kmeans.fit(idfb[cluster_columns2])
idfb[f"cluster2"] = kmeans.predict(idfb[cluster_columns2])
idfc = pd.DataFrame(
kmeans.cluster_centers_.tolist(), columns=cluster_columns
)
idfc.sort_values(cluster_columns[1], inplace=True)
idfc[f"reCluster2"] = list(range(sub_ncls*n_cls))
idfb[f"cluster2"] = idfb[f"cluster2"].map(
idfc[f"reCluster2"].to_dict())
dflist += [idfb]
dfclist += [idfc]
idfc = pd.concat(dfclist, ignore_index=True)
# label_lastC_rateが低い順にクラスを分け直す
clsnames2 = [f"{g}{i}" for g in clsnames for i in range(sub_ncls)]
idfc = idfc.sort_values(cluster_columns[1], ignore_index=True)
idfc["Cname"] = [g for g in range(n_cls) for _ in range(sub_ncls)]
idfc.sort_values(["Cname", cluster_columns2[0]],
ignore_index=True, inplace=True)
new_cls_map = {old: new for old, new in zip(
idfc["reCluster2"].tolist(), clsnames2)}
idfc["reCluster3"] = idfc["reCluster2"].map(new_cls_map)
idfc
なんとなくうまくいってそう?
ということで、クラスタ分けの結果とクラスタ中心がどうなったかを確認してみる
idfAll = pd.concat(dflist, ignore_index=True)
idfAll["cluster2"] = idfAll["cluster2"].map(
idfc.set_index("reCluster2")["reCluster3"].to_dict())
plt.figure(figsize=(8, 6))
plt.rcParams["font.size"] = 11
g = sns.scatterplot(idfAll.drop_duplicates(cluster_columns), x="label_1C_rate",
y="label_lastC_rate", hue="cluster2", alpha=0.75, hue_order=idfc["reCluster3"].tolist())
# plt.vlines(x=0, ymax=2, ymin=-1, colors="black", alpha=0.5)
# plt.ylim(bottom=0.025, top=1.025)
# plt.xlim(left=-0.25, right=1.025)
plt.scatter(idfc[cluster_columns[0]],
idfc[cluster_columns[1]]/rate, marker="X", s=100, c="black", label="Center")
for txt, row in zip(clsnames2, idfc[cluster_columns].values):
plt.text(row[0], row[1]/rate, s=txt, c="black",
weight="bold", size="xx-large")
# plt.legend(loc="best")
sns.move_legend(g, "upper left", bbox_to_anchor=(
0.1, -0.1), title='cluster2', fontsize=11, ncol=4)
plt.grid(ls=":")
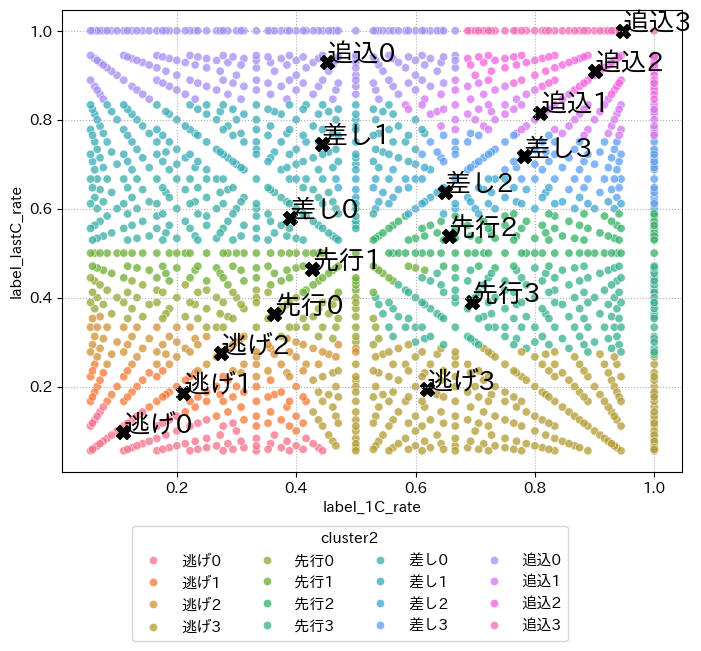
plt.show()
分布から「逃げ0」から「逃げ2」はlabel_lastC_rate, label_1C_rateがちょうど同じ値に近く値自身も小さい
よって、このクラスはレース序盤から逃げの戦法をとり最終コーナまで同じペースと位置を維持できるほどの能力が他の競走馬よりもあったことが分かる
一方で「追込1」から「追込3」では、さっきとは真逆でレースのペースについていけなかった競走馬であると考えられる
このクラスタリングのやり方でもまだ「先行」と「差し」の区別が難しい状態ではあるがlabel_lastC_rateを基準に見れば「先行0」以外の「先行」グループは「差し」グループと区別がついているように見える
7-8.最終着順と脚質の関係¶
ではこのクラスタリング結果から最終着順が1着になっているクラスタの分布を確認する
idfAll["label_rate"] = idfAll["label"]/idfAll["horseNum"]
plt.figure(figsize=(32, 8), )
plt.rcParams["font.size"] = 18
params = {
"x": "label",
# "y":"clsName",
"hue": "cluster2",
# "bins": 7,
"multiple": "dodge",
# "kde": True,
"stat": "probability",
"hue_order": clsnames2
}
for num, dist in enumerate("SMILE", start=1):
plt.subplot(2, 5, num)
sns.histplot(
idfAll[idfAll["label"].isin([1]) & ~idfAll["field"].isin(["芝"]) & ~idfAll["dist_cat"].isin(
[dist])][cluster_columns+["label", "label_rate", "cluster2", "cluster"]],
**params,
legend=num == 6,
)
plt.ylim(0, 0.45)
plt.grid(ls=":")
plt.xticks([1], ["1着"])
plt.xlabel(f"芝-{dist}")
if dist == "E":
continue
flag = num == 4
plt.subplot(2, 5, 5+num)
g = sns.histplot(
idfAll[idfAll["label"].isin([1]) & ~idfAll["field"].isin(["ダ"]) & ~idfAll["dist_cat"].isin(
[dist])][cluster_columns+["label", "label_rate", "cluster2", "cluster"]],
**params,
legend=flag
)
plt.ylim(0, 0.45)
plt.grid(ls=":")
plt.xticks([1], ["1着"])
plt.xlabel(f"ダ-{dist}")
if flag:
sns.move_legend(g, "upper left", bbox_to_anchor=(
1.0, 1), title='cluster2', fontsize=14, ncol=4)
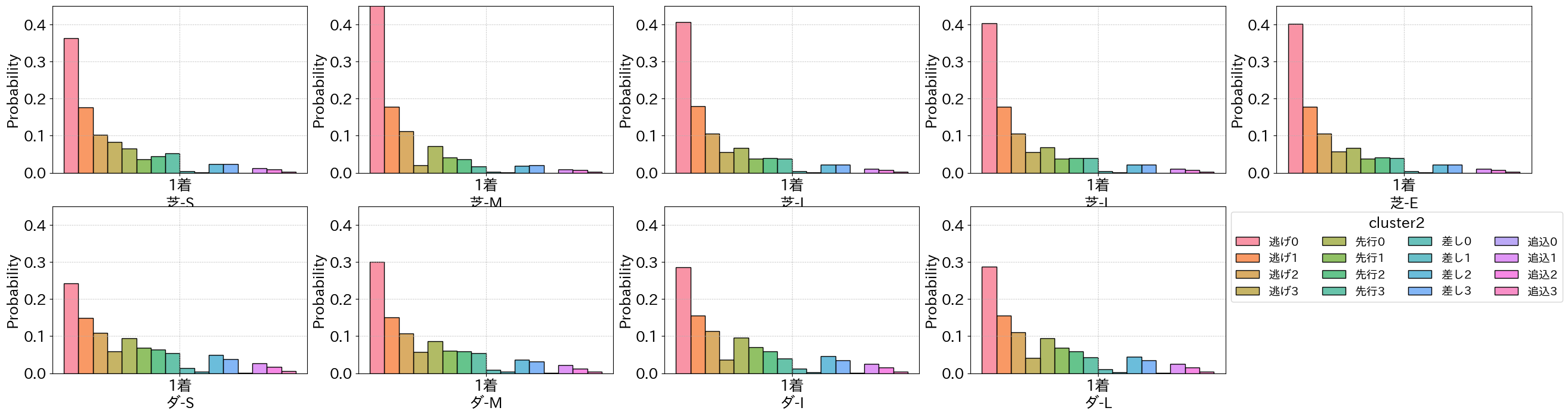
plt.show()
結果からやはり最終コーナを上位で通過した競走馬はゴールに近い分、1着になる割合が高いことが分かる
この傾向は馬場や距離カテゴリ別で見ても同じであることから、最初に逃げの戦法をとる競走馬が有利であることが分かる
クラスタリングの分け方が多すぎるので、末尾の数字を切って「逃げ」「先行」「差し」「追込」の4種類に減らして1着になる割合を確認する
idfAll["clsName"] = idfAll["cluster2"].str[:-1]
plt.figure(figsize=(32, 8), )
plt.rcParams["font.size"] = 18
params = {
"x": "label",
# "y":"clsName",
"hue": "clsName",
# "bins": 7,
"multiple": "dodge",
# "kde": True,
"stat": "probability",
"hue_order": clsnames
}
for num, dist in enumerate("SMILE", start=1):
plt.subplot(2, 5, num)
sns.histplot(
idfAll[idfAll["label"].isin([1]) & ~idfAll["field"].isin(["芝"]) & ~idfAll["dist_cat"].isin(
[dist])][cluster_columns+["label", "label_rate", "clsName"]],
**params,
legend=num == 6,
)
plt.ylim(0, 1)
plt.grid(ls=":")
plt.xticks([1], ["1着"])
plt.xlabel(f"芝-{dist}")
if dist == "E":
continue
flag = num == 4
plt.subplot(2, 5, 5+num)
g = sns.histplot(
idfAll[idfAll["label"].isin([1]) & ~idfAll["field"].isin(["ダ"]) & ~idfAll["dist_cat"].isin(
[dist])][cluster_columns+["label", "label_rate", "clsName"]],
**params,
legend=flag
)
plt.ylim(0, 1)
plt.grid(ls=":")
plt.xticks([1], ["1着"])
plt.xlabel(f"ダ-{dist}")
if flag:
sns.move_legend(g, "upper left", bbox_to_anchor=(
1.0, 1), title='clsName', fontsize=14, ncol=4)
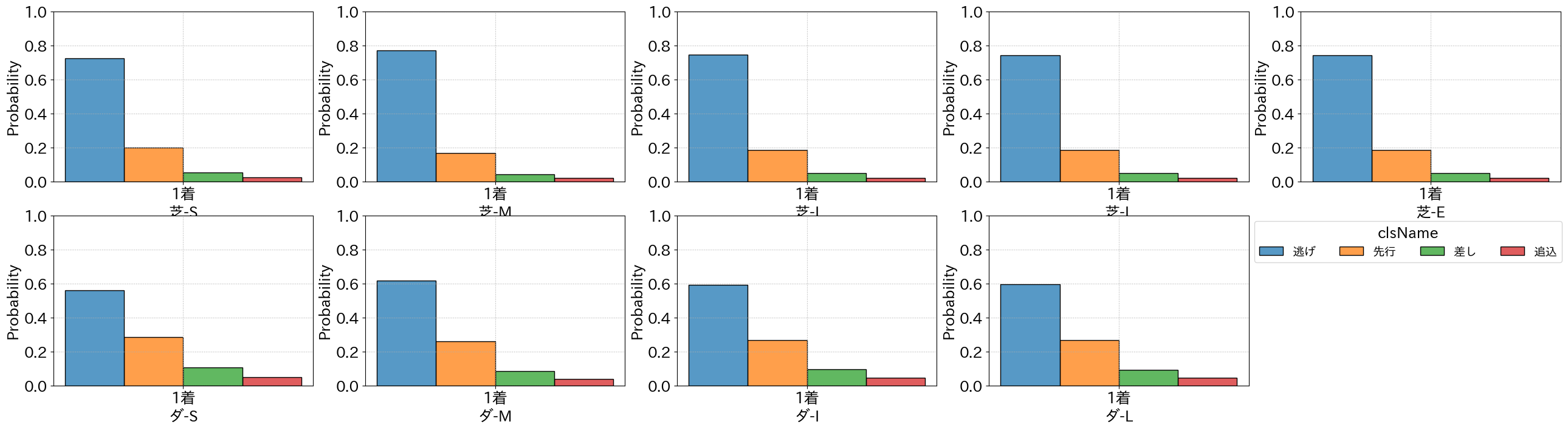
plt.show()
逃げの脚質の競走馬が1着になる競走馬の中で6割から最大8割にものぼることが分かる
つまり、勝てる競走馬を割り出すには出走馬の中から最終コーナを上位で回れるものを予測するのが重要そうだと分かった
ちなみに、逃げの脚質の競走馬の回収率も見てみる
for col in clsnames:
idfa = idfAll[idfAll["cluster2"].str.contains(col)]
p_list = []
for idx in range(sub_ncls):
iidfa = idfa[idfa["cluster2"].isin([f"{col}{idx}"])]
p_list += [
{
"脚質": f"{col}{idx}",
"収益": iidfa[iidfa["label"].isin([1])]["odds"].sum(),
"ベット数": len(iidfa),
"回収率": iidfa[iidfa["label"].isin([1])]["odds"].sum()/len(iidfa)
}
]
p_list += [
{
"脚質": f"{col}",
"収益": idfa[idfa["label"].isin([1])]["odds"].sum(),
"ベット数": len(idfa),
"回収率": idfa[idfa["label"].isin([1])]["odds"].sum()/len(idfa)
}
]
display(pd.DataFrame(p_list).set_index("脚質").convert_dtypes().T)
逃げの脚質だけ十分収益を出せることが分かる
※これはレース結果をもとに割り振った脚質を使っての分析なので、予想モデル作成では使えない情報であることに注意
7-9.クラスタリング結果の使い方
脚質の分析から1着の競走馬を予測したい ⇒ 「逃げ」の脚質を予測したいと言い換えて考えてみる
どう考えればいいか?¶
過去の成績からどの脚質に割り振られるかを分類できると良いのではないか?
大事なことは脚質とはレース中の戦法であるので、これまでのファーストモデルやセカンドモデルのように競走馬自身の情報+レース情報だけで得た1着になる確信度を予測するモデルでは不十分だということ。
つまり、他の競走馬を考慮してレース中の戦法を取るので、脚質の分類を考えたい場合はレースに出走する競走馬同士の情報を考慮する必要がある。
上記のような考え方の場合、思いつくのがニューラルネットワークを用いた学習方法であるがこれまでの動画や記事の流れで行くと少し話が飛躍してしまう。
なので、ここではもう少しLightGBMをこすることにする。
LightGBMによるランキング学習アプローチ
- 特徴量: 競走馬の過去の脚質分布と出走する競走馬全体の脚質分布と出走馬たちの過去の走破速度など、脚質に関連しそうな情報を使う
- 目的変数: 2パターンを用意。「逃げ」「先行」「差し」「追込」の4クラスとさらに4クラスに細分化した16クラス
- タスク: ランク学習
ランク学習(/ランキング学習)とは?
回帰モデルや分類モデルでは、目的変数の値を直接求めようと学習する。
つまり、回帰モデルでは例えば競走馬の走破タイムを予測する場合、そのモデルはその競走馬の走破タイムを予想するという感じ。
しかし、ランク学習では目的変数同士の大小関係を学習する。
つまり、データAとデータBがある評価指標に基づきA>Bという関係があるとき、ランク学習ではA>Bとなるようにモデルを学習する。
なので、損失関数はA>Bとなるパラメータを良しとし、A<Bとなるパラメータに罰則を与えるように学習する。
どのようにランク学習するかというと、LightGBMにはちょうどランク学習用のモデルが用意されているのでLightGBMを使ってやるのが手っ取り早い。
通常、ランク学習はクエリと呼ばれる一つのグループごとにデータ間の大小を学習していくのも、競馬予想というタスクでも非常に都合がいい
なぜランク学習?¶
ランク学習は目的変数の大小関係を学習するものであること、そして今回の目的は脚質4種類(または16種類)を予測するものである。
そもそも脚質というのはレース中の戦法であり出走中の出走位置を示す。
そのため、この脚質というものには「逃げ」>「先行」>「差し」>「追込」という順序関係が存在している。
そしてこの順序はレースごとに決まるものなので、レースごとに目的変数の大小関係を学習できるランク学習がうってつけである。
7-10.LightGBMによる脚質の予測¶
7-9節の話から、脚質を予測するランク学習のLightGBMモデルを作成する
特徴量の作成
脚質に関係しそうな指標が必要であるが、それらは過去の成績から分かるものという前提を置く。
過去成績から
レースごとに競走馬の過去の脚質や走破速度の集計をしないといけないが正直かなり大変
泥臭いがやってみることにする
dflist = []
mode = "clsName"
modelist = clsnames
dfg = idfAll[["horseId", "raceId", "raceDate",
"field", "dist_cat"]].groupby("raceId")
dfhg = idfAll[["horseId", "raceId", "raceDate",
"field", "dist_cat"]].groupby("horseId")
idfa = idfAll[["horseId", "raceId", "raceDate", "field", "dist_cat", mode]]
# 処理数を減らすために2014年のデータから集計する
for raceId in tqdm.tqdm(idfAll[["raceDate", "raceId"]][idfAll["raceDate"].dt.year > 2013]["raceId"].sort_values().unique()):
dfrace = dfg.get_group(raceId)
raceDate: datetime.datetime = dfrace["raceDate"].unique()[0]
field = dfrace["field"].unique()[0]
dist_cat = dfrace["dist_cat"].unique()[0]
idfh = idfa[idfa["horseId"].isin(dfrace["horseId"].tolist()) & idfa["field"].isin([
field]) & idfa["dist_cat"].isin([dist_cat])]
idfh: pd.DataFrame = idfh[idfh["raceDate"] < raceDate]
if len(idfh) > 0:
horseList = sorted(idfh["horseId"].unique())
dfcls = (idfh.groupby("horseId")[mode].value_counts(
)/idfh.groupby("horseId")[mode].count())
dfcls = pd.concat([dfcls.loc[hId].to_frame(hId)
for hId in horseList], axis=1).T.reset_index(names="horseId").fillna(0)
dfcls["raceId"] = raceId
dfclsAll = (idfh[mode].value_counts()/len(idfh)
).rename(lambda x: f"ALL{x}").to_frame().T
dfclsAll["raceId"] = raceId
dfcls = dfcls.set_index(["raceId", "horseId"]).reset_index()
dfcls = pd.merge(dfrace[["raceId", "horseId"]], dfcls, on=[
"raceId", "horseId"], how="left")
dfcls = pd.merge(dfcls, dfclsAll, on="raceId", how="left")
dflist += [dfcls]
else:
dflist += [dfrace[["raceId", "horseId"]]]
# break
if raceDate.year == 2015:
break
dffeature = pd.concat(dflist, ignore_index=True)
1年間のループで9分程度かかる
少なくとも2014年以降のデータを処理するのだから、まともに逐次処理をしたら1時間以上はかかってしまう
さすがに待ってられないので、並列処理を行う関数を用意した
notebookに関数を記載して並列処理はどう頑張っても無理なので、競馬予想AIプログラムのソースに並列処理用の関数を作成した
この並列処理で作成する特徴量は以下
- 過去の成績から分類した脚質の分布を計算
以下は本ソース↓を入手しないと実行できないので注意ください
from src.multi_func_utils.quantile_past_velosity import multi_exec_for_notebook
mode = "clsName"
modelist = clsnames
# mode = "cluster2"
# modelist = clsnames2
dffeature = multi_exec_for_notebook(
mode,
2014,
2021,
idfAll[[mode, "horseId", "raceId", "last3F_vel",
"toL3F_vel", "raceDate", "field", "dist_cat"]],
256,
10
)
自分の環境で9分程度で終わる
かなり便利なので、活用ください
もう少し整理して学習できる形までもっていく
# 説明変数
feature_columns = [
"raceId",
"breedId", "bStallionId", "b2StallionId", "stallionId",
"field", "dist_cat", "distance", "place", "condition",
"clsLabel_lag1", "clsLabel_lag2", "clsLabel_lag3", "clsLabel_lag4", "clsLabel_lag5",
"clsLabel_lag6", "clsLabel_lag7", "clsLabel_lag8", "clsLabel_lag9", "clsLabel_lag10",
"last3F_vel_lag1", "last3F_vel_lag2", "last3F_vel_lag3",
"toL3F_vel_lag1", "toL3F_vel_lag2", "toL3F_vel_lag3",
"raceGrade", "raceGrade_diff1",
]+dffeature.columns.tolist()[2:]
dflabel = idfAll[["raceDate", "raceId", "raceDetail", "jockeyId", "horseId", "favorite", "clsName", "label", "cluster2",
"field", "dist_cat", "distance", "place", "condition", "odds", "raceGrade", "last3F_vel", "toL3F_vel", "label_1C", "label_lastC"]]
for col in ["horseId", "breedId", "bStallionId", "b2StallionId", "stallionId"]:
idfAll[col] = idfAll[col].astype(str)
dffl = pd.merge(dflabel, dffeature, on=[
"raceId", "horseId"], how="left").fillna(0)
for col in ["breedId", "bStallionId", "b2StallionId", "stallionId"]:
dffl[col] = dffl["horseId"].map(idfAll.set_index("horseId")[col].to_dict())
dffl
以上で説明変数と目的変数を持つDataFrameに変換できた
agg_list = ["field", "dist_cat"]
dfcheck = dffl[["raceId"]+agg_list+dffeature.columns.tolist()[len(modelist):] +
["last3F_vel", "toL3F_vel"]]
dfc = dfcheck.groupby("raceId")[
["last3F_vel", "toL3F_vel"]].mean().reset_index()
dfcheck = pd.merge(dfc, dfcheck.drop_duplicates(
"raceId", ignore_index=True)[["raceId"]+agg_list+dffeature.columns.tolist()[-len(modelist):]],
on="raceId", how="left")
dfcagg = dfcheck.groupby(agg_list)[
["last3F_vel", "toL3F_vel"] +
dffeature.columns[-len(modelist):].tolist()].corr()[
["last3F_vel", "toL3F_vel"]].reset_index(level=len(agg_list), names=[0, 0, "mode"])
display(dfcagg[dfcagg["mode"].isin(dffeature.columns[-len(modelist):])
].loc["芝"].loc[[s for s in "SMILE"]].T)
display(dfcagg[dfcagg["mode"].isin(dffeature.columns[-len(modelist):])
].loc["ダ"].loc[[s for s in "SMIL"]].T)
ランク学習の実行
# ラベル作成
clsnames2_map = {col: num for num, col in enumerate(modelist)}
dffl["clsLabel"] = dffl[mode].map(clsnames2_map)
dffl.sort_values("raceDate", inplace=True, ignore_index=True)
for col in ["clsLabel", "last3F_vel", "toL3F_vel"]:
for num in range(1, 11):
dffl[f"{col}_lag{num}"] = dffl.groupby(
"horseId")[col].shift(num).fillna(len(clsnames2_map) if col == "clsLabel" else 100)
dffl["raceGrade"] = dffl["raceGrade"].astype(int)
dffl[f"raceGrade_diff{1}"] = dffl.groupby(
"horseId")["raceGrade"].shift(1).fillna(len(clsnames2_map))
cat_list = [
"horseId", 'jockeyId', "field", "place", "dist_cat",
"condition", "breedId", "bStallionId", "b2StallionId", "stallionId",
"clsLabel_lag1", "clsLabel_lag2", "clsLabel_lag3", "clsLabel_lag4",
"clsLabel_lag5", "clsLabel_lag6", "clsLabel_lag7",
"clsLabel_lag8", "clsLabel_lag9", "clsLabel_lag10",
]
for col in cat_list:
dffl[col] = dffl[col].astype("category")
# データセットの作成
dffl = dffl[~dffl["raceDetail"].str.contains(r"新馬|未出走", regex=True)]
dftrain, dfvalid, dftest = dffl[dffl["raceId"].str[:4] <= "2019"], dffl[dffl["raceId"].str[:4].isin(
["2020"])], dffl[dffl["raceId"].str[:4].isin(["2021"])]
train_data = lgbm.Dataset(
dftrain[feature_columns[1:]], label=len(clsnames2_map)-dftrain["clsLabel"],
group=dftrain.groupby("raceId")["raceId"].count().values)
valid_data = lgbm.Dataset(
dfvalid[feature_columns[1:]], label=len(clsnames2_map)-dfvalid["clsLabel"],
group=dfvalid.groupby("raceId")["raceId"].count().values)
test_data = lgbm.Dataset(dftest[feature_columns[1:]], label=len(clsnames2_map)-dftest["clsLabel"],
group=dftest.groupby("raceId")["raceId"].count().values)
# ハイパーパラメータ
params = {
'objective': 'lambdarank',
'metric': 'ndcg',
"categorical_feature": cat_list,
'ndcg_eval_at': [1, 2, 5, 6, 9, 10, 13, 14],
'boosting_type': 'gbdt',
'seed': 77777,
}
# モデル学習
model = lgbm.train(params, train_data, num_boost_round=1000, valid_sets=[
train_data, valid_data], callbacks=[
lgbm.early_stopping(
stopping_rounds=50, verbose=True,),
lgbm.log_evaluation(25 if True else 0)
],)
学習が完了したがモデルの予測結果は分類モデルと違い、グループごとの大小関係しか出さない
そのため、予測結果からランク付けを改めて行わなければならない。
ランク付け=脚質の振り分けと同じ
学習では「逃げ」>「先行」>「差し」>「追込」といった大小関係を学習させていたので、モデルの予測結果が高いものであればあるほど「逃げ」に近い脚質になることを期待し、逆であれば「追込」に近い脚質になることを期待するように予測しているということである。
ランク付けの方針は
- レースごとに予測確度の最大値と最小値を計算
- 学習データの方で割り出したクラスごとの割合を用いて割り振る
詳細はcalc_pred関数を参照
dftrain["pred_proba"] = model.predict(
dftrain[feature_columns[1:]], num_iteration=model.best_iteration)
q_map = (dftrain[mode].value_counts() /
dftrain[mode].count()).sort_values().values.cumsum()[:-1]
q_map
def calc_pred(df1, q_map=q_map):
df1["pred"] = len(clsnames2_map)-1
df1["pred_max"] = df1["raceId"].map(df1.groupby(
"raceId")["pred_proba"].max().to_dict())
df1["pred_min"] = df1["raceId"].map(df1.groupby(
"raceId")["pred_proba"].min().to_dict())
for q in q_map:
df1["pred_q"] = df1["pred_min"] + (df1["pred_max"]-df1["pred_min"])*q
df1["pred"] -= (df1["pred_proba"] > df1["pred_q"]).astype(int)
return df1
df1 = dftest
df1["pred_proba"] = model.predict(
df1[feature_columns[1:]], num_iteration=model.best_iteration)
df1 = calc_pred(df1)
raceId = np.random.choice(df1["raceId"])
df1[df1["raceId"].isin([raceId])][[
"raceId", "field", "place", "dist_cat",
"favorite", "odds", "label", "pred",
"pred_proba", "clsLabel",
"label_lastC", "label_1C",
]+dffeature.columns.tolist()[2:]]
dfvalid["pred_proba"] = model.predict(
dfvalid[feature_columns[1:]], num_iteration=model.best_iteration)
dfvalid = calc_pred(dfvalid)
dftest["pred_proba"] = model.predict(
dftest[feature_columns[1:]], num_iteration=model.best_iteration)
dftest = calc_pred(dftest)
pd.concat([dftest["clsLabel"].value_counts().rename("真値").sort_index().to_frame().T,
dftest["pred"].value_counts().rename("予測値").sort_index().to_frame().T])
dft = dftest # [(dftest["pred_proba"] > 1/len(clsnames2_map))]
idfheat = pd.concat([(dft[["clsLabel", "pred"]].groupby("pred")["clsLabel"].value_counts(
)/dft[["clsLabel", "pred"]].groupby("pred")["clsLabel"].count()).loc[num]
for num in range(len(clsnames2_map))], axis=1).sort_index()
idfheat
pd.concat([(dft[["label", "pred"]].groupby("pred")["label"].value_counts(
)/dft[["label", "pred"]].groupby("pred")["label"].count()).loc[num]
for num in range(len(clsnames2_map))], axis=1).sort_index().head(10)
idfg = dfvalid
print("検証データ")
for name, i in clsnames2_map.items():
idft = idfg[idfg["pred"].isin([i])]
idft1 = pd.merge(idft[["raceId", "horseId", "pred", "pred_proba"]],
idfAll, on=["raceId", "horseId"], how="inner")
idft1 = idft1[~idft1["raceGrade"].isin([0, 1, 2, 3, 4, 5])]
print(
f'Cluster: {i}-{name},\t{round(idft1[idft1["label"].isin([1])]["odds"].sum(),1)},' +
f'\t{len(idft1)},\t{idft1["label"].isin([1]).sum()},' +
f'\t{round(idft1["label"].isin([1,]).mean(), 3)},' +
f'\t{round(idft1[idft1["label"].isin([1])]["odds"].sum()*100/len(idft1), 2)}'
)
idfg = dftest
print("テストデータ")
for name, i in clsnames2_map.items():
idft = idfg[idfg["pred"].isin([i])]
idft1 = pd.merge(idft[["raceId", "horseId", "pred", "pred_proba"]],
idfAll, on=["raceId", "horseId"], how="inner")
idft1 = idft1[~idft1["raceGrade"].isin([0, 1, 2, 3, 4, 5])]
print(
f'Cluster: {i}-{name},\t{round(idft1[idft1["label"].isin([1])]["odds"].sum(),1)},' +
f'\t{len(idft1)},\t{idft1["label"].isin([1]).sum()},' +
f'\t{round(idft1["label"].isin([1,]).mean(), 3)},' +
f'\t{round(idft1[idft1["label"].isin([1])]["odds"].sum()*100/len(idft1), 2)}'
)
何度か試してほしいけど、シードに関わらず結構結果が変わってしまうようである。
自分の環境で実行したときのある時の結果を以下に出し、以降はこの結果をもとに話す。
検証データ Cluster: 0-逃げ, 475.5, 567, 46, 0.081, 83.86 Cluster: 1-先行, 826.5, 503, 41, 0.082, 164.31 Cluster: 2-差し, 255.9, 390, 27, 0.069, 65.62 Cluster: 3-追込, 342.6, 439, 14, 0.032, 78.04
テストデータ Cluster: 0-逃げ, 687.1, 552, 56, 0.101, 124.47 Cluster: 1-先行, 337.0, 531, 36, 0.068, 63.47 Cluster: 2-差し, 165.1, 387, 17, 0.044, 42.66 Cluster: 3-追込, 246.6, 438, 20, 0.046, 56.3
検証データとテストデータで結果がバラバラ、一貫性がない、これでは意味がない。
ただ、脚質を予想すれば的中率を上げられるヒントがあるかもしれない。
最後に重要度を確認して締めくくる
pd.DataFrame(model.feature_importance(
"gain").tolist(), index=feature_columns[1:]).round(2).sort_values(0)


コメント