はじめに¶
私は競馬予想AIの開発をしています。動画で制作過程の解説をしています。良ければ見ていってください。

また、共有するソースの一部は有料のものを使ってます。
同じように分析したい方は、以下の記事から入手ください。

8.過去成績からレース展開の予測
前回は脚質の分析とその予測の可能性を見てきた。
今回の話では、各出走馬の過去成績による脚質の変遷と持ちタイムからレース展開の予測を試みる。
レース展開を知りたい理由は、戦法の一つである脚質がレース展開によって勝ちやすい負けやすいといった話が一般的にあり、そういった影響も勝ち馬を絞り込む上では重要な要素となる可能性が十分ありうるからである。
そのため、レース展開の予測ができるかどうかを調べることは必要であると考える。
8-1.話の内容
- 持ちタイムの分析
- レース展開の分析
- レース展開の予測
8-2.前提の話: レース展開(ペース情報)って?¶
GPTに聞いてみた結果が以下
競馬のレース展開にはさまざまなパターンがある。以下はいくつかの典型的な例である。馬の特徴やペース、コースの形状などによって、展開が異なることがある。
1. 逃げ切り(逃げ馬有利)¶
逃げ馬が最初からリードを取り、そのままペースを維持してゴールまで先頭を守る展開である。特に前残りの馬場や短距離戦でよく見られる。逃げ馬にとってはスタミナよりもスピードと持続力が重要である。
- 例: スプリントレース(1200m前後) では、スタートから勢いよく飛び出して、最後まで先頭をキープすることが多い。
2. 差し馬の台頭¶
レースの中盤から後方でじっと我慢していた馬が、直線に入ってから加速し、先行馬を次々と交わしていく展開である。差し馬に有利な展開は、前半のペースが速く、逃げや先行馬がバテやすい状況でよく見られる。
- 例: 中距離レース(1800m – 2400m) では、ペースが落ち着くことが多く、終盤の差し馬が活躍する場面が増える。
3. 追い込み(追い込み馬の豪脚)¶
レースの後方で待機していた馬が、最後の直線で猛烈なスピードを見せて一気に追い込み、ゴール直前で逆転する展開である。これは特に長距離戦やペースが速く、前がバテた展開で見られる。
- 例: 長距離レース(2400m以上) では、追い込み馬が最後に爆発的な脚を使って一気に追い上げることがしばしばある。
4. ペースメーカーの存在による展開¶
時にはレースのペースを乱すために、あえて逃げ馬や先行馬にペースを上げさせる「ペースメーカー」として出走する馬が存在する。このような馬の存在によって、他の馬が早めに仕掛けざるを得なくなり、後ろから差す馬が有利になる展開である。
5. 団子状態のレース¶
全体的にペースが遅く、馬群が固まったまま直線に入る展開である。この場合、どの馬もチャンスがあり、抜け出すタイミングが重要になる。位置取りや騎手の判断力が勝敗を分けることが多い。
6. ハイペースからのバテ合い¶
レース序盤から中盤にかけてペースが速すぎる場合、逃げや先行馬がバテてしまい、最終的には後方待機馬が有利になる展開である。特に前に行った馬たちが早いペースに巻き込まれたとき、終盤の粘りがなくなり、後続の馬たちが一気に追い込む展開がよくある。
これらの展開のパターンは、馬場状態、天候、出走馬の脚質、距離などに影響されることも多い。競馬ファンとしては、これらの展開を読みながら予想を楽しむことが、競馬の醍醐味の一つである。
上記のレース展開例から以下の5ケースのレース展開がありうるのではと考える
- 速いペース × 逃げが勝ち切り
- 速いペース × 逃げが負ける
- 遅いペース × 逃げが勝ち切り
- 遅いペース × 逃げが負ける
- 脚質の影響がないケース
以上の5ケースを知るためにもう少し話を嚙み砕いて、レース展開を予想する上では以下2つに着目すると良いのではと考えた。
一つ目に、逃げ馬や人気馬の影響によってペースの速い遅いが決まるのではないか
(逃げ馬が多いレースはどの馬も前に行きたがるので、ペースが速くなるのでは)
二つ目に、先頭集団と後方集団とのパワーバランスによって逃げの勝ち負けが決まるのではないか
(ペースの速い遅いに関わらず先頭集団の能力が高ければ、後方が差せない場合があり、逆のパターンもあるのでは)
つまり、逃げ馬と他競走馬の関係を知ることが重要だと考えた。
上記の話から、まずはレースのペースを知る必要がありそう。
そのためには、レース出走時点での各馬のペース情報と脚質が鍵になってきそう。
なので、まず最初に持ちタイムの分析から始めていく。
8-3.前準備¶
ソースの一部は有料のものを使ってます。
同じように分析したい方は、以下の記事から入手ください。
import pathlib
import warnings
import lightgbm as lgbm
import pandas as pd
import tqdm
import datetime
import matplotlib.pyplot as plt
import japanize_matplotlib
import seaborn as sns
import numpy as np
import sys
sys.path.append(".")
sys.path.append("..")
from src.data_manager.preprocess_tools import DataPreProcessor # noqa
from src.data_manager.data_loader import DataLoader # noqa
warnings.filterwarnings("ignore")
root_dir = pathlib.Path(".").absolute().parent
dbpath = root_dir / "data" / "keibadata.db"
start_year = 2000 # DBが持つ最古の年を指定
split_year = 2014 # 学習対象期間の開始年を指定
target_year = 2019 # テスト対象期間の開始年を指定
end_year = 2023 # テスト対象期間の終了年を指定 (当然DBに対象年のデータがあること)
# 各種インスタンスの作成
data_loader = DataLoader(
start_year,
end_year,
dbpath=dbpath # dbpathは各種環境に合わせてパスを指定してください。絶対パス推奨
)
dataPreP = DataPreProcessor()
df = data_loader.load_racedata()
dfblood = data_loader.load_horseblood()
df = dataPreP.exec_pipeline(
df, dfblood, ["s", "b", "bs", "bbs", "ss", "sss", "ssss", "bbbs"])
8-4.持ちタイムの分析¶
8-4-0.持ちタイムとはなにかを決める
ここではまず出走馬たちの持ちタイムとレースのペース情報との関係を見てみる
ということで、持ちタイムの情報になりそうなデータがどのカラムに入っているのか思い出す
df.columns
タイム関連情報は以下のカラムになりそう
time: 出走タイムlast3F: 上り3Fタイムvelocity: 60 × レース距離 / 出走タイムlast3F_vel: 600 / 上り3FタイムtoL3F_vel: 上り3Fに到達するまでの速度
そもそも持ちタイムとは「同じ距離のレースの中で最も速かったタイムのこと」と考えられることが多い。
しかし、レース距離や条件などで色々変わったりすることも考慮が必要であると考える。
また、最後の上り3Fはこれまでのペースに関わらず全速力で走ることが要求されると思われるので、上り3Fに至るまでの速度を持ちタイムと見た方がペースを予測する上では重要ではないかと考える。
よってここでは、持ちタイムを以下に定義する。
- 持ちタイム
- 馬場×レース距離×馬齢ごとの最速の
toL3F_velの値とする - ただし、欠損値は前出のデータで埋めるとする。
- つまり、4歳になって初めて出走した
- 芝のマイル距離レースの持ちタイムは、
- 3歳までに出走していた同条件のレースの
- 持ちタイムで埋め合わせる
8-4-1.持ちタイムの求め方
DataFrameのgroupbyを活用しつつ、shiftメソッドとrollingメソッドを使って求める。
horseId×field×distance×ageでgroupbyして、
最大過去100レースに対するtoL3F_velカラムの最大値を計算
欠損値をなるべく減らすために、馬齢が変わって初めて出走するレース条件では、
一つ前の馬齢での同条件の持ちタイムで埋め合わせる
それでも欠損が出る場合は、以下の優先度の特徴量ごとに
過去成績の最小値を出して埋める(悲観的評価を採用する)
horseId×field×distancehorseId×field×dist_cathorseId×field
targetCol = "toL3F_vel"
idf = df.copy()
idf = idf[~idf["horseId"].isin(
idf[idf["horseId"].str[:4] < "1998"]["horseId"].unique())]
idf["mochiTime_org"] = idf.groupby(['horseId', "field", "distance", "age"])[
targetCol].shift()
idf["mochiTime"] = idf.groupby(['horseId', "field", "distance", "age"])["mochiTime_org"].rolling(
1000, min_periods=1).max().reset_index(level=[0, 1, 2, 3], drop=True)
idf["mochiTime_org"] = idf.groupby(['horseId', "field", "distance"])[
targetCol].shift()
idf["mochiTime"].fillna(idf.groupby(['horseId', "field", "distance"])["mochiTime_org"].rolling(
1000, min_periods=1).min().reset_index(level=[0, 1, 2], drop=True), inplace=True)
idf["mochiTime_org"] = idf.groupby(['horseId', "field", "dist_cat"])[
targetCol].shift()
idf["mochiTime"].fillna(idf.groupby(['horseId', "field", "dist_cat"])["mochiTime_org"].rolling(
1000, min_periods=1).min().reset_index(level=[0, 1, 2], drop=True), inplace=True)
idf["mochiTime_org"] = idf.groupby(['horseId', "field",])[
targetCol].shift()
idf["mochiTime"].fillna(idf.groupby(['horseId', "field"])["mochiTime_org"].rolling(
1000, min_periods=1).min().reset_index(level=[0, 1], drop=True), inplace=True)
targetCol = "last3F_vel"
idf = idf[~idf["horseId"].isin(
idf[idf["horseId"].str[:4] < "1998"]["horseId"].unique())]
idf["mochiTime_org"] = idf.groupby(['horseId', "field", "distance", "age"])[
targetCol].shift()
idf["mochiTime3F"] = idf.groupby(['horseId', "field", "distance", "age"])["mochiTime_org"].rolling(
1000, min_periods=1).max().reset_index(level=[0, 1, 2, 3], drop=True)
idf["mochiTime_org"] = idf.groupby(['horseId', "field", "distance"])[
targetCol].shift()
idf["mochiTime3F"].fillna(idf.groupby(['horseId', "field", "distance"])["mochiTime_org"].rolling(
1000, min_periods=1).min().reset_index(level=[0, 1, 2], drop=True), inplace=True)
idf["mochiTime_org"] = idf.groupby(['horseId', "field", "dist_cat"])[
targetCol].shift()
idf["mochiTime3F"].fillna(idf.groupby(['horseId', "field", "dist_cat"])["mochiTime_org"].rolling(
1000, min_periods=1).min().reset_index(level=[0, 1, 2], drop=True), inplace=True)
idf["mochiTime_org"] = idf.groupby(['horseId', "field",])[
targetCol].shift()
idf["mochiTime3F"].fillna(idf.groupby(['horseId', "field"])["mochiTime_org"].rolling(
1000, min_periods=1).min().reset_index(level=[0, 1], drop=True), inplace=True)
8-4-2.持ちタイムと走破タイムの関連
出走前に算出した持ちタイムと走破タイムに関連があるかの確認
簡単に散布図でみる
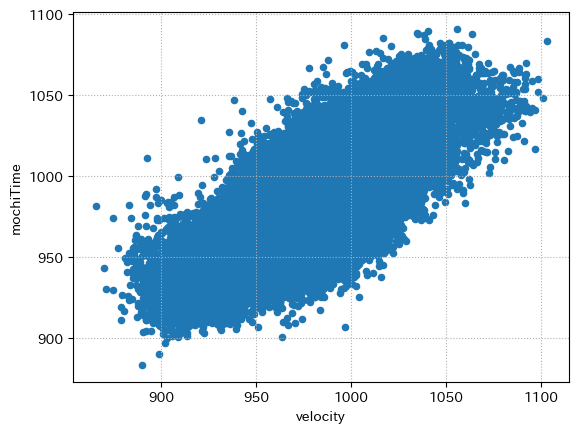
idf2 = idf.groupby("raceId")[["velocity", "mochiTime"]].mean()
idf2.plot.scatter("velocity", "mochiTime")
plt.grid(ls=":")
plt.show()
当たり前かもだが、恐ろしく相関がある
つまり、持ちタイムを見れば走破タイムを予想可能である可能性が高い
8-4-3.持ちタイムと着順の関係
それなら、レースごとに持ちタイムが最も速い競走馬が1着になるのか?
ということなので、持ちタイムが最速の競走馬の着順分布と、
それ以外の競走馬の着順分布を確認する
出走数の違いもあると思うので、それぞれ割合でみる
idf["mochiRank"] = idf.groupby("raceId")["mochiTime"].rank(ascending=False)
idfdes = pd.concat(
[
idf[idf["mochiRank"] < 2]["label"].value_counts().rename("top1") /
len(idf[idf["mochiRank"] < 2]),
idf[idf["mochiRank"] >= 2]["label"].value_counts().rename(
"other")/len(idf[idf["mochiRank"] >= 2]),
],
axis=1
).T
display(idfdes)
idfdes.T.plot()
plt.grid(ls=":")
plt.show()
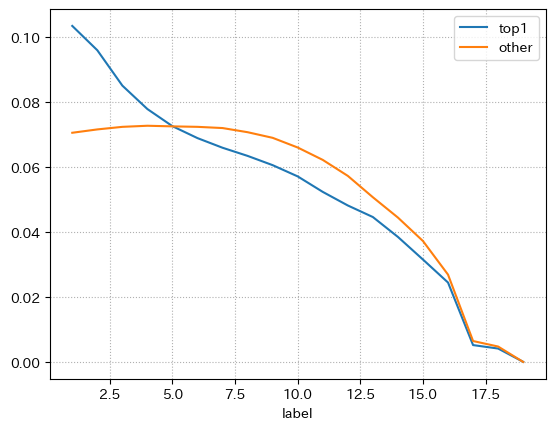
もともと出走する競走馬の数もレースごとに違うので、10着以降の分布は割合の数字に意味はない。
結果を見るに、持ちタイム最速は、そうでないものとで1着になりやすい
もう少し細かく見たい
持ちタイムが1位, 2位, 3位, 4位, 5位とそれ以外でみる
idf["mochiRank"] = idf.groupby("raceId")["mochiTime"].rank(ascending=False)
idf["mochiRank"] = idf["mochiRank"].apply(
lambda d: d if pd.isna(d) else int(d))
idfdes = pd.concat(
[
idf[idf["mochiRank"].isin([i])]["label"].value_counts().rename(f"top{i}") /
len(idf[idf["mochiRank"].isin([i])])
for i in range(1, 6)
] + [
idf[idf["mochiRank"] >= 6]["label"].value_counts().rename(
"other")/len(idf[idf["mochiRank"] >= 6])
],
axis=1
).T
display(idfdes)
idfdes.T.plot()
plt.grid(ls=":")
plt.show()
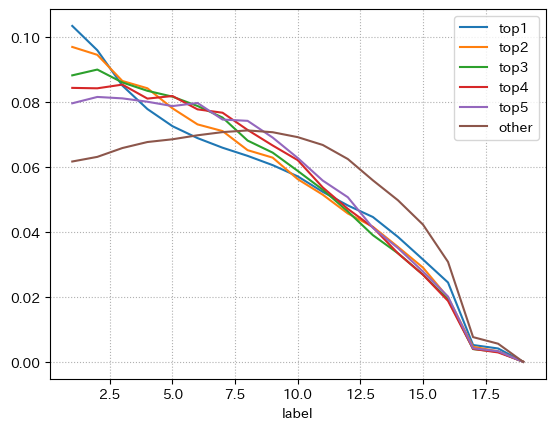
1着から2着あたりまで序列通りであるが、3着以降になると逆転している
心なしか曲線もtop5に行くにつれて、otherと同じ曲がり方(上に凸という)になる。
top1のみ下に凸な曲がり方をしている
8-4-4.持ちタイムと人気の関係
無論ここまで関係しているのであれば、
持ちタイムが最速であれば自ずと人気も集中しているだろうという推測がたつ
さっきと同じような分布を人気版として出す
idf["mochiRank"] = idf.groupby("raceId")["mochiTime"].rank(ascending=False)
idf["mochiRank"] = idf["mochiRank"].apply(
lambda d: d if pd.isna(d) else int(d))
idfdes = pd.concat(
[
idf[idf["mochiRank"].isin([i])]["favorite"].value_counts().rename(f"top{i}") /
len(idf[idf["mochiRank"].isin([i])])
for i in range(1, 6)
] + [
idf[idf["mochiRank"] >= 6]["favorite"].value_counts().rename(
"other")/len(idf[idf["mochiRank"] >= 6])
],
axis=1
).T
display(idfdes)
idfdes.T.plot()
plt.grid(ls=":")
plt.show()
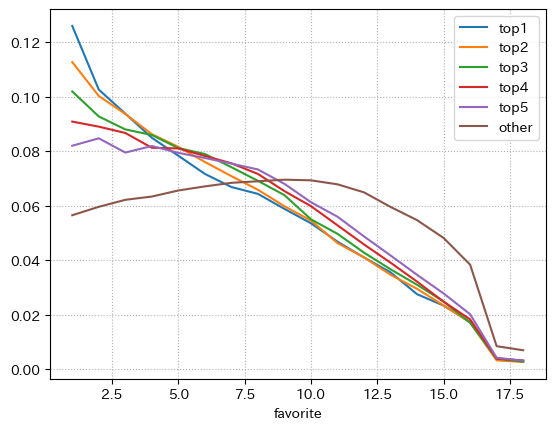
見立て通り持ちタイム最速の競走馬の1番人気が多い。
しかし、中には5番人気以降になっているデータも少なからずある。
これは欠損値の埋合せなどが影響しているか、別の原因でそう判断されているのか定かではない
要するに足の速い競走馬は当然ながら成績を残すし人気も集まりやすい
ただし、それ以外の不安要素が見つかるとその限りではない
という一般的な考え方に当てはまる結果であると考える。
8-4-5.ペース情報の分析¶
持ちタイムの速さとレースのペース情報の前半と後半のタイムから関係を見る
ペース情報に関するカラムは「rapTime」が該当する
idfpace = idf.drop_duplicates(
"raceId", ignore_index=True) # 処理しやすいように重複を削除しておく
idfpace[["raceId", "rapTime"]]
これは200mごとのラップタイムになっているため、上り3Fを除いた前半と後半の200mの平均ラップタイムを割り出すとレースのペースが見えてくるのではと考える
レース距離が奇数の場合は、最初の100mのラップタイムを取るので注意。(1150mのレースもあるので注意)
idfpace["rapTime2"] = idfpace[["rapTime", "distance"]].apply(
lambda row: row["rapTime"] if row["distance"] % 200 == 0
else [round(row["rapTime"][0]*200/(row["distance"] % 200), 1)] + row["rapTime"][1:], axis=1)
idfpace[idfpace["distance"].isin([1150])][["rapTime", "rapTime2"]]
idfpace["prePace"] = idfpace["rapTime2"].apply(
lambda lst: np.mean(lst[:(len(lst)-3)//2]))
idfpace["pastPace"] = idfpace["rapTime2"].apply(
lambda lst: np.mean(lst[(len(lst)-3)//2:-3]))
idfpace["prePace3F"] = idfpace["rapTime2"].apply(
lambda lst: np.mean(lst[:-3]))
idfpace["pastPace3F"] = idfpace["rapTime2"].apply(
lambda lst: np.mean(lst[-3:]))
idfpace[["raceId", "rapTime2", "prePace", "pastPace"]]
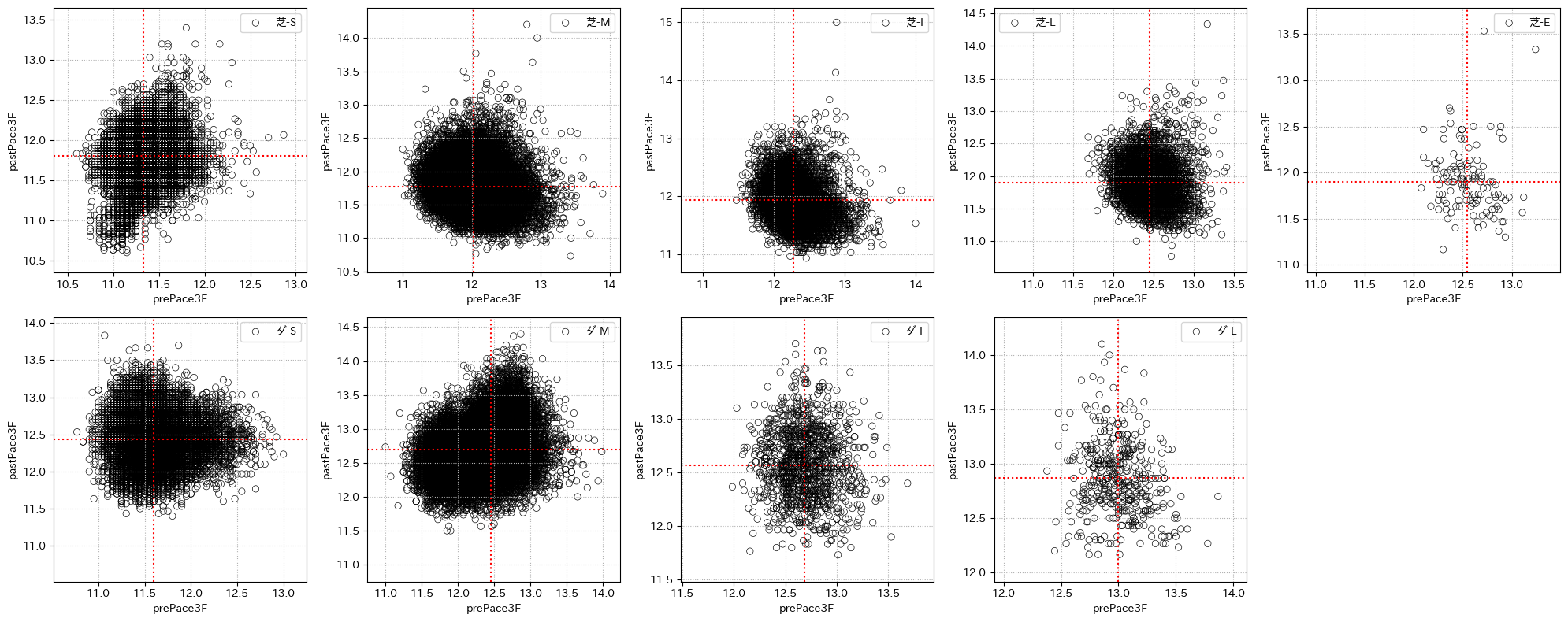
xcol = "prePace3F"
ycol = "pastPace3F"
plt.figure(figsize=(20, 8))
for n, f in enumerate(["芝", "ダ"], start=0):
for m, d in enumerate("SMILE", start=1):
idfp = idfpace[idfpace["field"].isin(
[f]) & idfpace["dist_cat"].isin([d]) & ~idfpace["raceId"].str[:4].isin(["2024", "2023", "2022"])]
if len(idfp) == 0:
continue
# region plot
minV = min(idfp[ycol].min(), idfp[xcol].min())
plt.subplot(2, 5, int(5*n+m))
sns.scatterplot(
idfp,
x=xcol,
y=ycol,
label=f"{f}-{d}",
edgecolors="black", facecolors="none"
)
plt.hlines(
idfp[ycol].median(),
xmin=minV-0.25,
xmax=idfp[xcol].max()+0.25,
colors="red",
linestyles=":"
)
plt.xlim(
left=minV-0.25,
right=idfp[xcol].max()+0.25
)
plt.vlines(
idfp[xcol].median(),
ymin=minV-0.25,
ymax=idfp[ycol].max()+0.25,
colors="red",
linestyles=":"
)
plt.ylim(
bottom=minV-0.25,
top=idfp[ycol].max()+0.25
)
plt.grid(ls=":")
# endregion
plt.tight_layout()
plt.show()
# 出力結果は省略する
if 0:
for d in ['函館', '福島', '新潟', '東京', '中山', '中京', '京都', '阪神', '小倉', '札幌', ]:
print("競馬場:", d)
plt.figure(figsize=(15, 6))
for n, f in enumerate(["芝", "ダ"], start=0):
for m, dist in enumerate("SMILE", start=1):
idfp = idfpace[idfpace["field"].isin(
[f]) & idfpace["place"].isin([d]) & ~idfpace["raceId"].str[:4].isin(
["2024", "2023", "2022"]) & idfpace["dist_cat"].isin([dist])
]
if len(idfp) == 0:
continue
# region plot
minV = min(idfp[ycol].min(), idfp[xcol].min())
plt.subplot(2, 5, int(5*n+m))
sns.scatterplot(
idfp,
x=xcol,
y=ycol,
label=f"{f}-{dist}",
edgecolors="black", facecolors="none"
)
plt.hlines(
idfp[ycol].median(),
xmin=minV-0.25,
xmax=idfp[xcol].max()+0.25,
colors="red",
linestyles=":"
)
plt.xlim(
left=minV-0.25,
right=idfp[xcol].max()+0.25
)
plt.vlines(
idfp[xcol].median(),
ymin=minV-0.25,
ymax=idfp[ycol].max()+0.25,
colors="red",
linestyles=":"
)
plt.ylim(
bottom=minV-0.25,
top=idfp[ycol].max()+0.25
)
plt.grid(ls=":")
plt.legend(loc="best")
# endregion
plt.tight_layout()
plt.show()
8-4-6.持ちタイムとペース情報の関係
レースごとに出走馬のlast3F_vel, toL3F_vel, velocity, mochiTimeの平均値を計算
上記の平均値の情報とレースごとのペース情報の相関を確認する。
idfvel = idf.groupby("raceId")[
["last3F_vel", "toL3F_vel", "velocity", "mochiTime", "mochiTime3F"]].mean().rename(columns=lambda x: f"{x}_mean").reset_index()
idfvel = pd.merge(idfpace[[
"raceId", "prePace", "prePace3F", "pastPace", "pastPace3F",]], idfvel, on="raceId")
idfvel.corr().loc[["mochiTime_mean", "mochiTime3F_mean"]]
結果から出走馬の持ちタイムの平均値であるmochiTime_meanに対してpastPace3F, pastPace, toL3F_vel_meanで0.8の相関がある。
つまり、出走馬の持ちタイム(速度指標)が速くなると後半のペース情報であるpastPaceが早くなり、出走馬の上り3Fに至るまでの速度の平均であるtoL3F_vel_meanが速くなることを意味する。
先では出走馬の平均情報とペース情報の関係をみた。
つぎは、各馬の持ちタイムと前走でのvelocity, last3F_vel, toL3F_velとレース結果のvelocity, last3F_vel, toL3F_velとの相関を確認する。
idf["vel_lag1"] = idf.groupby("horseId")["velocity"].shift()
idf["l3Fvel_lag1"] = idf.groupby("horseId")["last3F_vel"].shift()
idf["t3Fvel_lag1"] = idf.groupby("horseId")["toL3F_vel"].shift()
idf[["velocity", "last3F_vel", "toL3F_vel", "vel_lag1",
"l3Fvel_lag1", "t3Fvel_lag1", "mochiTime", "mochiTime3F"]].corr().loc[
["vel_lag1", "l3Fvel_lag1", "t3Fvel_lag1", "mochiTime", "mochiTime3F"]][["velocity", "last3F_vel", "toL3F_vel"]]
持ちタイムでみると上り3F到達までの速度であるtoL3F_velと0.67の相関がある。
これは前走の同指標であるt3Fvel_lag1(前走のtoL3F_vel)とtoL3F_velの相関0.61よりも高い。
前走のtoL3F_velの情報よりも、持ちタイムの方が上り3Fに到達するまでの情報と関係がありそうということである。
idfp = pd.merge(
idf[["raceId",]+list(set(idf.columns) - set(idfvel.columns))],
idfvel[["raceId", "last3F_vel_mean", "toL3F_vel_mean",
"mochiTime_mean", "mochiTime3F_mean"]],
on="raceId"
)
idfp
次にレースごとの持ちタイムの平均値と上り3F持ちタイムの平均値とレース結果のlast3F_velとtoL3F_velの平均値を各指標から引いたmochiTime_diff, mochiTime3F_diff, last3F_diff, toL3F_diffの相関係数を見る。
この平均値を引く操作は、レースごとに競走馬の情報から共通する情報(平均値)を抜き出すことで純粋な各競走馬のみの情報だけにする効果がある。
こうすることで、持ちタイムが他出走馬よりも高い場合にlast3F_diff, toL3F_diffが同じ関係にあるのかどうかを確認することができる。
idfp["mochiTime_diff"] = idfp["mochiTime"] - idfp["mochiTime_mean"]
idfp["mochiTime3F_diff"] = idfp["mochiTime3F"] - idfp["mochiTime3F_mean"]
idfp["last3F_diff"] = idfp["last3F_vel"] - idfp["last3F_vel_mean"]
idfp["toL3F_diff"] = idfp["toL3F_vel"] - idfp["toL3F_vel_mean"]
idfp[["last3F_diff", "toL3F_diff", "mochiTime_diff", "mochiTime3F_diff"]].corr(
).loc[["mochiTime_diff", "mochiTime3F_diff"]][["last3F_diff", "toL3F_diff"]]
結果からmochiTime_diffがtoL3F_diffに対して相関が0.23とやや関係があるが、last3F_diffとはほとんど関係がないことが分かった。(上り3Fについても同様)
つまりこれはmochiTimeが他競走馬よりも高くとも最後の上り3Fでぶっちぎれるとは限らないが、上り3Fに達するまでの間はやや優勢であることを意味する。
8-5.持ちタイムと脚質の関係¶
レース当日の出走馬の脚質(=戦法)は、出走馬同士の持ちタイムとこれまでの脚質の趣向を見て騎手が判断するものと考えられる。
ここでの目標は、持ちタイムと過去の脚質から当日の脚質の予測精度の改善を目指す。
8-5-0.まずは脚質の分類を行う¶
流れとしては、クラスタ用の特徴量を準備して前回のクラスタ結果をもとにKmeansモデルを作ってクラスタリングする。
まずはクラスタ用の特徴量の作成とKMeansモデルの初期化
from sklearn.cluster import KMeans # KMeans法のモジュールをインポート
for col in ["label_1C", "label_lastC"]:
idfp[f"{col}_rate"] = (idfp[col].astype(
int)/idfp["horseNum"]).convert_dtypes()
# クラスタ数
n_cls = 4
rate = 2.5
# クラスタリングする特徴量を選定
cluster_columns = ["label_1C_rate", "label_lastC_rate"]
cluster_columns2 = ["label_1C_rate", "label_lastC_rate2"]
kmeans = KMeans(n_clusters=n_cls) # 脚質が4種類なので、クラス数を4とする
idfp["label_lastC_rate2"] = rate*idfp["label_lastC_rate"]
# 後でクラスタ中心を振り直すが、形式上一旦fitしておかないといけない。
kmeans.fit(idfp[cluster_columns2].iloc[:n_cls*2])
KMeans(n_clusters=4)
以下でクラスタ中心をセットして、クラスタリングを実行
※非推奨なやり方かもしれないので、気になる場合は前回の「0007_past_results_analyze.ipynb」で行っていた順序でクラスタするとよい
# クラスタ中心をセット
centers = [
[0.189736, 0.393819],
[0.432436, 0.995918],
[0.639462, 1.612348],
[0.836256, 2.227643]
]
kmeans.cluster_centers_ = np.array(centers)
# 脚質の分類
idfp["cluster"] = kmeans.predict(idfp[cluster_columns2])
# 名前も付けておく
clsnames = ["逃げ", "先行", "差し", "追込"]
cls_map = {i: d for i, d in enumerate(clsnames)}
idfp["clsName"] = idfp["cluster"].map(cls_map)
idfp["clsName"].value_counts().to_frame().T
このようにクラスタ中心さえ分かっていれば、KMeansのモデルの保存を行わずともモデルの読み込みができるので再現性を取ることができます。
8-5-1.脚質と持ちタイムの分析¶
脚質ごとに持ちタイムやレース出走速度の指標についての統計情報を確認する
corrList = ["mochiTime", "mochiTime3F", "mochiTime_diff",
"mochiTime3F_diff", "last3F_diff", "toL3F_diff"]
for col in corrList:
display(idfp.groupby("clsName")[[col]].describe().loc[clsnames])
ちょっと判断が難しいので、多群間の差を検定するクラスカルウォリス検定を使う
from scipy.stats import kruskal
for col in corrList:
datalist = []
for clsn in clsnames:
datalist += [idfp[idfp["clsName"].isin([clsn])][col].dropna().values]
print(f"対象: {col},\t\t", "検定結果:", kruskal(*datalist))
一応多群での有意差は認められたが、この検定の欠点はどの群とどの群、つまりどの脚質とどの脚質で差があるのかを教えてはくれない。
この場合多重検定を行う必要があり、2群の全組合せの検定(マンホイットニーのU検定)をした後にボンフェローニ補正による調整が必要になる。
import statsmodels.stats.multitest as smm
from itertools import combinations
from scipy.stats import mannwhitneyu
for col in corrList:
datalist = []
for cols in combinations(clsnames, 2):
x = idfp[idfp["clsName"].isin([cols[0]])][col].dropna().values
y = idfp[idfp["clsName"].isin([cols[1]])][col].dropna().values
datalist += [mannwhitneyu(x, y, alternative="greater").pvalue]
corrected_p_values = smm.multipletests(
datalist, alpha=0.05, method='bonferroni')
print(
f"対象: {col},\t",
f"有意か?: {corrected_p_values[0].all()},\t",
f"p値: {corrected_p_values[1].round(6)}"
)
結果からすべての2群の組合せに対してmochiTime_diffとtoL3F_diffで有意差があり、p値も十分に小さいことが分かった。
とりわけ過去データである持ちタイムの情報(mochiTime_diff)が、レース結果から分かる脚質においてグループ間で差異があるという結果は非常にありがたいことである。
8-5-2.持ちタイムと前走の脚質の分析¶
とりあえずペース情報の追加
idf = pd.merge(idfp, idfpace[["raceId", "prePace",
"pastPace", "prePace3F", "pastPace3F"]], on="raceId")
前回の話で脚質をランク学習で分類する方法を紹介した。
その分類するモデルについて、特徴量重要度を確認したところ最も重要だと判断されていたのが前走の脚質情報だった。
前回の脚質分類モデルの特徴量重要度
| 0 | |
|---|---|
| 一部抜粋 | ・・・ |
| last3F_vel_lag1 | 2268.75 |
| clsLabel_lag7 | 2355.62 |
| toL3F_vel_lag1 | 3380.81 |
| distance | 3479.48 |
| clsLabel_lag6 | 4548.93 |
| raceGrade | 6348.59 |
| clsLabel_lag5 | 6371.05 |
| bStallionId | 9171.27 |
| b2StallionId | 10189.09 |
| clsLabel_lag4 | 13089.48 |
| stallionId | 16163.15 |
| clsLabel_lag3 | 21275.96 |
| clsLabel_lag2 | 59780.57 |
| breedId | 66164.67 |
| clsLabel_lag1 | 187454.07 |
脚質を分類するついでに持ちタイムと前回の脚質情報等からレース展開であるペース情報の推測に役立てられないかを考えたい
まずは前5走分の脚質情報を作る。
for lag in range(1, 6):
idf[f"clsName_lag{lag}"] = idf.sort_values("raceDate").groupby("horseId")[
"clsName"].shift(lag)
ついでに前走の脚質情報と持ちタイム等の有意性をみる
for col in corrList+["toL3F_vel"]:
datalist = []
for cols in combinations(clsnames, 2):
x = idf[idf["clsName_lag1"].isin([cols[0]])][col].dropna().values
y = idf[idf["clsName_lag1"].isin([cols[1]])][col].dropna().values
datalist += [mannwhitneyu(x, y, alternative="greater").pvalue]
corrected_p_values = smm.multipletests(
datalist, alpha=0.05, method='bonferroni')
print(
f"対象: {col},\t",
f"有意か?: {corrected_p_values[0].all()},\t",
f"p値: {corrected_p_values[1].round(6)}"
)
ということで、前走の脚質情報でもmochiTimeとmochiTime_diffの指標で順序関係の有意差があると考える。
つまり、前走が逃げと先行の2馬だと統計的にmochiTimeが逃げ>先行の関係であるということである。
更には、toL3F_diffやtoL3F_velで有意差があることから前走の脚質情報によって上り3Fに至るまでの速度が違うことが分かる。
ペース情報は決まった距離ごとのラップタイムの平均で算出することから、これは前走の脚質情報によってペース情報を知ることが出来得ると考える。
idf.groupby("clsName_lag1")[
["mochiTime", "mochiTime_diff"]].mean().loc[clsnames]
実際に平均でみてもそうであると分かる。
これを手掛かりに脚質×持ちタイムを使ってペース情報の推測が出来ないか探る。
8-5-3.持ちタイム×前5走の脚質とペース情報の分析¶
改めてペース情報の確認
prePace: 残り600mを除いたスタートからの前半の200mペース情報pastPace: 残り600mを除いたprePaceからの後半の200mペース情報prePace3F: 残り600mまでの200mペース情報pastPace3F: 残り600mの200mペース情報
目標としては前5走の脚質情報と持ちタイムからペース情報の割り出しを目指したい。
なぜなら、ペース情報を知ることで出走馬がそのペースについていけるかどうかを判断できると競馬予想に大きく役立てられると考えるからである。
まずは、先ほど前5走データの脚質情報を追加したので、レースごとの出走馬の前5走データから脚質情報を集約して各脚質の割合を算出する。
このようにすることで、出走馬の前5走の脚質の平均的な分布を知ることができると考えた。
つまり、出走馬の前5走のほとんどが逃げの脚質だと、全体の逃げの割合が増えるためレースのペースも上がるのではと考える。
dflist = {}
lagcolumns = ["clsName_lag1", "clsName_lag2",
"clsName_lag3", "clsName_lag4", "clsName_lag5"]
for g, dfg in tqdm.tqdm(idf[["raceId",] + lagcolumns].groupby("raceId")):
dflist[g] = (pd.Series(dfg[lagcolumns].values.reshape(-1)
).value_counts() / dfg[lagcolumns].notna().sum().sum()).to_dict()
dfcls = pd.DataFrame.from_dict(dflist, orient="index")
idfp = pd.merge(idf, dfcls.reset_index(names="raceId"), on="raceId")
idfp3 = idfp.set_index(["field", "distance"])
idfp3["prePace3F_diff"] = idfp[["field", "distance",
"prePace3F"]].groupby(["field", "distance"])["prePace3F"].mean()
idfp["prePace3F_diff"] = idfp["prePace3F"] - \
idfp3["prePace3F_diff"].reset_index(drop=True)
レースごとに脚質の割合から各タイム関連情報との相関を見る
idfp[["prePace", "pastPace", "prePace3F", "pastPace3F", "raceGrade", "prePace3F_diff", "toL3F_vel_mean"] +
clsnames].corr().loc[["prePace", "pastPace", "prePace3F", "pastPace3F", "raceGrade", "prePace3F_diff", "toL3F_vel_mean"]][clsnames]
結果から特徴的なのは、先行の脚質の割合が高くとも低くともペース情報には関係がない結果になっている
他の脚質ではprePace3FやtoL3F_vel_meanなど上り3Fに至るまでのタイム関連情報に対して相関が0.3から0.4程度とやや関係があるように見える。
実際にprePace3Fと逃げと追込の脚質の割合との関係をグラフで見てみる
for cn in clsnames[0::3]:
xcol = cn
ycol = "prePace3F"
plt.figure(figsize=(15, 4))
minVx = min(idfp[xcol].min(), idfp[xcol].min()) - 0.1
minVy = min(idfp[ycol].min(), idfp[ycol].min())*0.99
maxVx = max(idfp[xcol].max(), idfp[xcol].max()) + 0.1
maxVy = max(idfp[ycol].max(), idfp[ycol].max())*1.01
for n, f in enumerate(["芝", "ダ"], start=0):
for m, dist in enumerate("SMILE", start=1):
idfp2 = idfp[
idfp["field"].isin([f]) &
~idfp["raceId"].str[:4].isin(["2024", "2023", "2022"]) &
idfp["dist_cat"].isin([dist])
].drop_duplicates([xcol, ycol]).sort_values("clsName", key=lambda data: [{v: -k for k, v in cls_map.items()}[x] for x in data]) # .groupby("clsName")[[xcol, ycol]].mean()
if len(idfp2) == 0:
continue
linear = np.polyfit(idfp2[idfp2[xcol].notna()][xcol].tolist(),
idfp2[idfp2[xcol].notna()][ycol].tolist(), 1)
linear_fn = np.poly1d(linear)
# region plot
plt.subplot(2, 5, int(5*n+m))
sns.scatterplot(
idfp2,
x=xcol,
y=ycol,
label=f"{f}-{dist}",
# hue="clsName",
edgecolors="black", facecolors="none",
# alpha=0.5
)
plt.plot(np.arange(0, 1.05, 0.05), linear_fn(
np.arange(0, 1.05, 0.05)), color="green")
plt.hlines(
idfp2[ycol].median(),
xmin=minVx,
xmax=maxVx,
colors="red",
linestyles=":"
)
plt.xlim(
left=minVx,
right=maxVx
)
plt.vlines(
idfp2[xcol].median(),
ymin=minVy,
ymax=maxVy,
colors="red",
linestyles=":"
)
plt.ylim(
bottom=minVy,
top=maxVy
)
plt.grid(ls=":")
plt.legend(loc="best")
# endregion
plt.tight_layout()
plt.show()
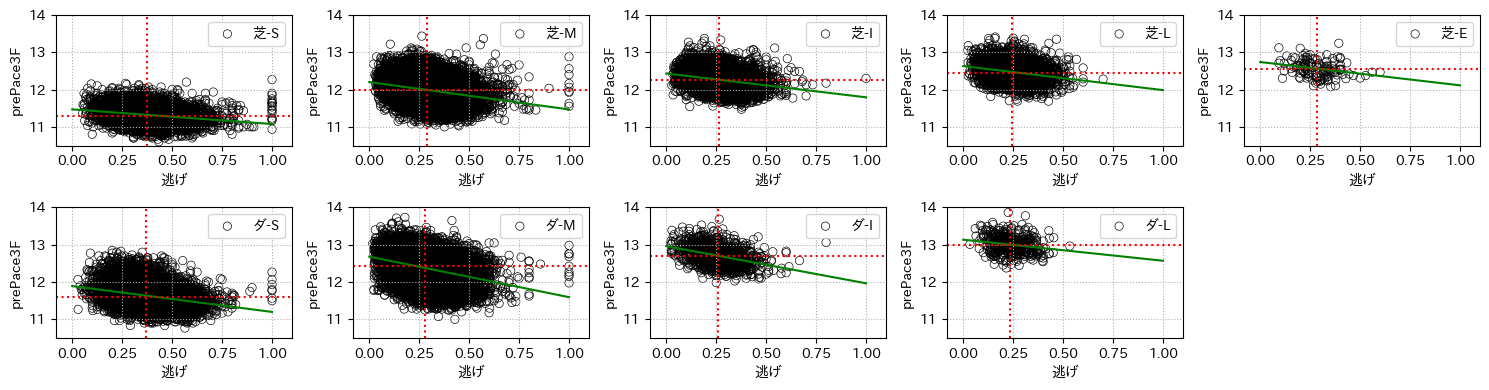
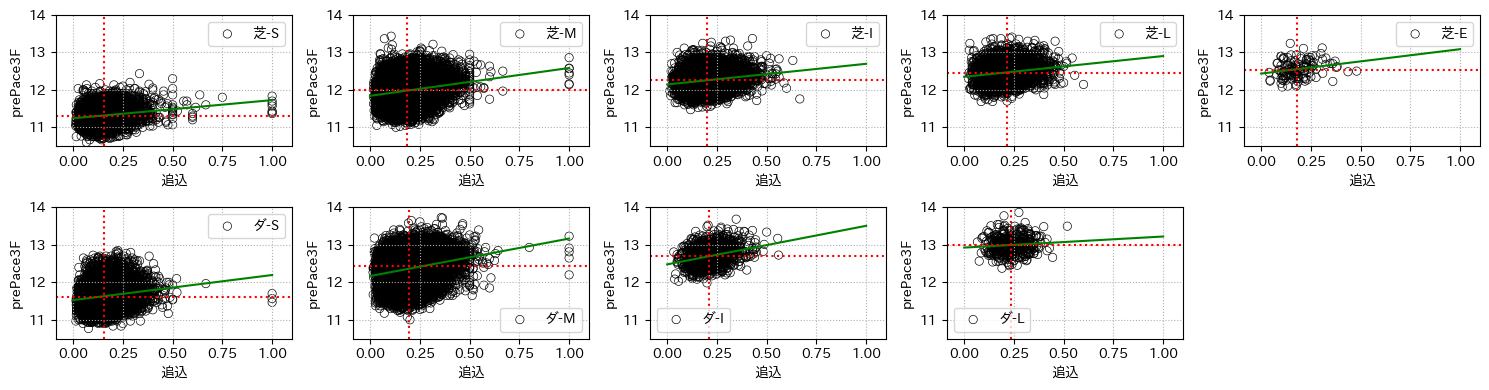
1つ目のグラフは横軸に出走馬の逃げの脚質の割合と縦軸にレース結果であるprePace3Fとしたグラフで、2つ目のグラフは横軸が追込となったものである。
赤線は各軸に対する中央値で、緑線は線形フィットしたものである
グラフの形を見ればわかるように、逃げの割合のグラフでは右肩下がりに追込の場合は右肩上がりとなっている。
つまり、逃げの割合が高くなると上がり3Fに至るまでのタイムが早くなり、追込みの割合が高くなると遅くなるということである。
これは当初に挙げたペース情報の一般的な解釈(8-2節)と一致することがわかる。
8-6.持ちタイム×前走の脚質を使ってペース情報の推定
先の分析で前走データの脚質の割合からペース情報の推定ができそうである。
よってLightGBMを使った回帰モデルでペース情報の推定を試みる。
8-6-1.LightGBMのモデル作成案¶
- モデル:回帰モデル
- 目的変数:
残り600m地点に到達するまでの200m単位の出走タイムの推定 - 説明変数: 前走情報の脚質割合とmochiTimeの平均値、そのほかレース情報のカテゴリ
- 学習期間: 2014年~2019年
- 検証期間: 2020年
- テスト期間: 2021年
8-6-2.特徴量作成¶
feature_columns = clsnames + \
[
"field", "place", "dist_cat", "distance",
"condition", "raceGrade", "horseNum", "direction",
"inoutside", 'mochiTime_mean', 'mochiTime3F_mean',
'weather', 'mochiTime_mean_div', 'mochiTime3F_mean_div',
"mochiTime_diff", "mochiTime", "mochiTime3F",
"mochiTime_div", "mochiTime3F_div", "horseId", "breedId",
"bStallionId", "b2StallionId", "stallionId"
]+lagcolumns
label_column = "toL3F" # 新しく残り600m地点到達までの200m単位走破タイム
cat_list = [
"field", "place", "dist_cat", 'weather',
"condition", "direction", "inoutside", "horseId",
"breedId", "bStallionId", "b2StallionId", "stallionId"
]+lagcolumns
for cat in cat_list:
idfp[cat] = idfp[cat].astype("category")
idfp["mochiTime3F_mean_div"] = 200*60/idfp["mochiTime3F_mean"]
idfp["mochiTime_mean_div"] = 200*60/idfp["mochiTime_mean"]
idfp["mochiTime_div"] = 200*60/idfp["mochiTime"]
idfp["mochiTime3F_div"] = 200*60/idfp["mochiTime3F"]
# toL3F_velが走破速度(分速)になっているので、200m単位のタイムに変換
idfp["toL3F"] = 200*60/idfp["toL3F_vel"]
dffl = idfp[["raceId", "raceDate"]+feature_columns +
["prePace3F", "toL3F_vel_mean", "toL3F"]] # .drop_duplicates("raceId", ignore_index=True)
dffl
8-6-3.モデルの学習¶
params = {
'metric': 'rmse',
"categorical_feature": cat_list,
'boosting_type': 'gbdt',
'seed': 777,
}
dftrain, dfvalid, dftest = dffl[dffl["raceId"].str[:4] <= "2019"], dffl[dffl["raceId"].str[:4].isin(
["2020"])], dffl[dffl["raceId"].str[:4].isin(["2021"])]
train_data = lgbm.Dataset(
dftrain[feature_columns], label=dftrain[label_column])
valid_data = lgbm.Dataset(
dfvalid[feature_columns], label=dfvalid[label_column])
test_data = lgbm.Dataset(dftest[feature_columns], label=dftest[label_column])
# モデル学習
model = lgbm.train(params, train_data, num_boost_round=1000, valid_sets=[
train_data, valid_data], callbacks=[
lgbm.early_stopping(
stopping_rounds=50, verbose=True,),
lgbm.log_evaluation(25 if True else 0)
],)
8-6-4.推論結果の追加¶
dftrain["pred"] = model.predict(
dftrain[feature_columns], num_iteration=model.best_iteration)
dfvalid["pred"] = model.predict(
dfvalid[feature_columns], num_iteration=model.best_iteration)
dftest["pred"] = model.predict(
dftest[feature_columns], num_iteration=model.best_iteration)
8-6-5.特徴量重要度の確認¶
pd.DataFrame(model.feature_importance("gain"),
index=feature_columns, columns=["重要度"]).round(3).sort_values("重要度")
結果からレースごとの出走馬の持ちタイムの平均情報が最も重要であり、次にレース距離, 競馬場, 馬場, 母の血統, レースグレードと続いている。
8-6-6.回帰モデルの評価指標の確認¶
ここでは決定係数と平均二乗誤差をみる。
- 決定係数: モデルがどれだけデータをうまく説明しているかを示す。1に近いほど良いモデル
- 平均二乗誤差: 予測値と実測値の誤差の二乗平均を示す。大きな誤差を重視する指標
from sklearn.metrics import r2_score, mean_squared_error
for key, dfg in [("train", dftrain), ("valid", dfvalid), ("test", dftest)]:
print(
f"データ: {key}, \tR2: {r2_score(dfg[label_column], dfg['pred']):.5f}, \tMSE: {mean_squared_error(dfg[label_column], dfg['pred']):.5f}")
結果を見ると、決定係数の値がかなりよく、1に近ければそれだけ良い指標で普通は0.7を超えると十分良い結果だと言われていることもあり、値が0.78177とかなり良い値となっている。
つまり、ペース情報の予測はそれなりにうまくいっているといえる。
dft = pd.merge(idfp, dftest[["raceId", "horseId", "pred"]], on=[
"raceId", "horseId"])
ランダムにレース情報を確認してみる。
実際に予測結果のペース情報が出走馬の出走タイムに沿っているか確認する。
実態とは微妙に違うが、脚質情報(clsName)は最終コーナ通過時の順位が大きく寄与しているので、今回の予測結果の値が小さいとそれだけ逃げの脚質である可能性が高い。
dft["pred_rank"] = dft.groupby("raceId")["pred"].rank()
dft[dft["raceId"].isin(["202105020811"])][[
"clsName", "pred_rank", "label", "raceId", "raceName", "horseId", label_column, "pred", "label_1C_rate", "label_lastC_rate", "mochiTime_diff"]].sort_values("pred_rank")
なんとなくそれなりに割り振りができてそうか?
実際にpred_rankが1.0のもの(horseId=2016104470)では、脚質が逃げになっているのが分かる。
これはうまくいきすぎているとは思うが、上位3位まですべて逃げの脚質となっていることから、まぁ精度よく学習できていると思える。
しかし、6位や7位で追込の脚質がきていることから、幾分ブレがあるようである。
実際のクラスタ結果と今回の予測結果のランク分けに関連があるか確認する
dft[["cluster", "pred_rank"]].corr()
結果から相関が0.395308ほどとそれなりに関係があると分かる。
for col in ["pred"]:
datalist = []
for cols in combinations(clsnames, 2):
x = dft[dft["clsName"].isin([cols[0]])][col].dropna().values
y = dft[dft["clsName"].isin([cols[1]])][col].dropna().values
datalist += [mannwhitneyu(x, y, alternative="less").pvalue]
corrected_p_values = smm.multipletests(
datalist, alpha=0.05, method='bonferroni')
print(
f"対象: {col},\t",
f"有意か?: {corrected_p_values[0].all()},\t",
f"p値: {corrected_p_values[1].round(6)}"
)
一応検定してみると有意差が出ていることがわかる。(p値が微妙なものもあるが・・・)
つまり、予測タイムが早ければ早いほど実際に分類される脚質も逃げ > 先行 > 差し > 追込みの順になっているということである。
# region plot
dft["pred_q75"] = dft["raceId"].map(dft[["raceId", "pred_rank"]].groupby(
"raceId")["pred_rank"].quantile(0.75).to_dict())
dft["pred_q75"] = dft["pred_rank"] >= dft["pred_q75"]
dft[dft["pred_q75"]]["label"].value_counts().sort_index()
dft["pred_q25"] = dft["raceId"].map(dft[["raceId", "pred_rank"]].groupby(
"raceId")["pred_rank"].quantile(0.25).to_dict())
dft["pred_q25"] = dft["pred_rank"] <= dft["pred_q25"]
dft[dft["pred_q25"]]["label"].value_counts().sort_index()
idft = pd.concat(
[
dft[dft["pred_q25"]]["label"].value_counts(normalize=True).sort_index(
).to_frame().rename(columns={"proportion": "上位25%"}),
dft[dft["pred_q75"]]["label"].value_counts(normalize=True).sort_index(
).to_frame().rename(columns={"proportion": "下位75%"})
],
axis=1
)
(idft.sort_index(ascending=False).cumsum().sort_index(ascending=True).rename(
columns={"上位25%": "上位25%_累積", "下位75%": "下位75%_累積"}).rename(index=lambda x: x-1)).plot(ax=idft.plot.bar(alpha=0.5).twinx())
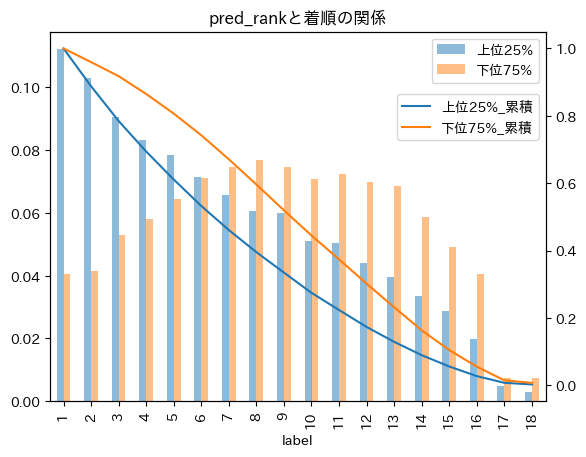
plt.title("pred_rankと着順の関係")
plt.legend(loc="upper right", bbox_to_anchor=(
1., 0.85),)
plt.show()
# endregion
グラフで比べてみると上位25%の方(青線)は累積分布の減り具合が早い(グラフがオレンジ線よりも下にきている)ため、下位75%よりも上位着順の割合が高いことを示している。
8-7.まとめ¶
分かったこと¶
前5走の脚質情報と持ちタイムを使った分析によって、各出走馬の走破タイムの推測ができそうだと分かった。
サードモデルで期待すること¶
過去成績から割り出した脚質情報と持ちタイムを特徴量として追加することでセカンドモデルよりも高いパフォーマンスを達成すること


コメント